Différé partiel
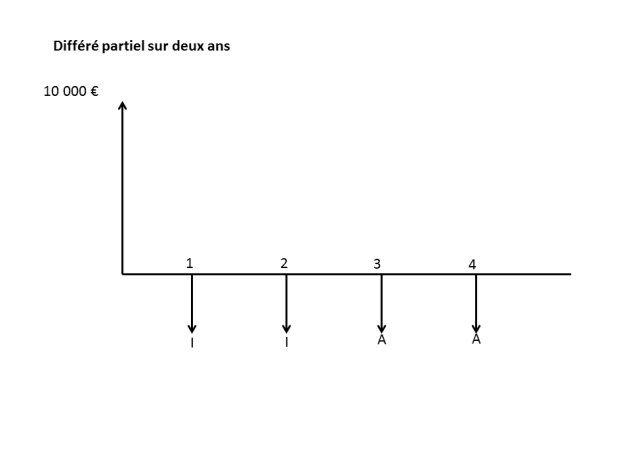
a) Diagramme des flux
Un emprunt de
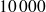€ consenti au taux de
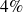annuels doit être remboursé en 4 ans.
Le remboursement de cet emprunt bénéficie d'un différé partiel sur deux ans, puis est effectué par annuités constantes.
Commentaire :
Les deux premières périodes, seuls les intérêts sont versés. Au cours de chacune de ces périodes, le capital restant dû reste égal au montant de l'emprunt. L'annuité A versée à la fin des deux dernières années permet d'amortir le capital dû au début de la troisième année.
b) Valeur de l'annuité
Valeur de l'annuité :
€
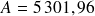Complément :
Calcul de l'annuité
:
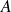Les deux premières années, le versement effectué en fin d'année est égal aux seuls intérêts soit
€.
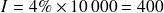Au début de la troisième année, le capital dû est
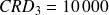€. Ce capital sera remboursé en deux annuités égales de valeur
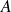telle que
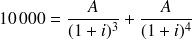et avec
,
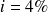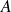doit vérifier :
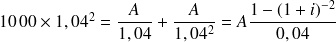
D'où le résultat :
€.
c) Tableau d'amortissement
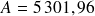d) Remarques
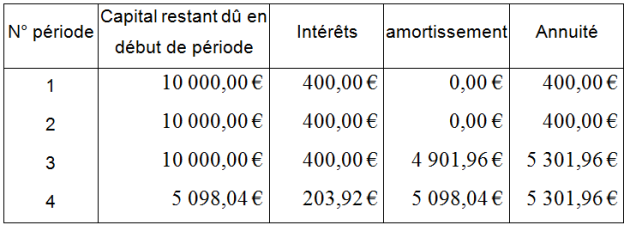
Les remarques faites à l'issue des différents échéanciers précédents restent valables.
• Sur la dernière ligne, l'amortissement est égal au capital restant dû en début de période.
• Si on calculait la somme des amortissements celle-ci serait égale au montant emprunté.
• Le coût de l'emprunt est égal à la somme des intérêts ou encore à la somme des annuités, diminuée du montant de l'emprunt.
