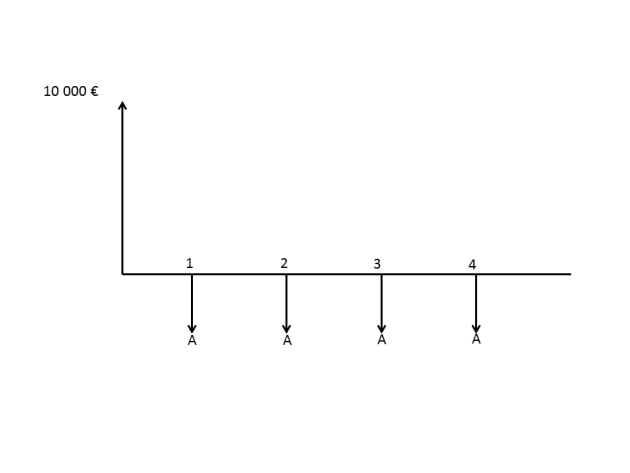
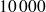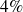Approfondissements
a) Diagramme des flux
Un emprunt de
€ consenti au taux de
annuels doit être remboursé en 4 ans.
L'amortissement du capital emprunté se fera par annuités constantes.
Commentaire :
Les versements sont identiques chaque période, mais la répartition entre capital et charge d'intérêt varie dans le temps.
b) Valeur de l'annuité :
€
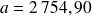Question
Comment calculer a ?
Calcul de l'annuité
:
permet l'équilibre du diagramme des flux autrement dit
est tel que :
Calcul de l'annuité a :
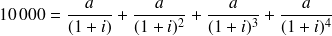ce qui s'écrit encore
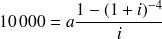et avec
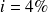, a doit vérifier :
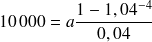
D'où le résultat :
€
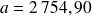c) Tableau d'amortissement
Pour chaque période, ce tableau précise l'intérêt dû et la part d'amortissement du capital dans l'annuité.
Important :
Les amortissements forment une suite géométrique de raison
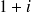et de premier terme
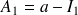
On peut le vérifier : en multipliant l'amortissement d'une période par
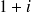c'est à dire par
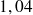, on obtient l'amortissement de la période suivante, et l'amortissement de la première période est
€.
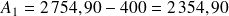Remarque
Ce tableau donne année après année
• le capital restant dû en début de période,
• les intérêts de la période
• l'amortissement du capital,
• l'annuité.
Il comporte donc 5 colonnes et 5 lignes, une ligne par année et une ligne supplémentaire portant les intitulés de colonne. La colonne 1, comporte les numéros de période, ici les années.
d) Comment construire le tableau d'amortissement
Important :
Il est utile de faire au moins un échéancier de ce type avec « papier, crayon » avant de faire des échéanciers de taille plus importante sur tableur, car ils sont construits de la même façon.
Question
Comment construire le tableau d'amortissement ?
Si pour la période k on note :
•
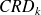le capital restant dû en début de période
•
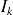l'intérêt dû,
•
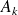l'amortissement,
•
l'annuité
on doit utiliser les formules :
•
•
•
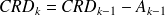
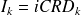
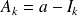
Ligne 1 :
Le capital restant dû en début de période 1 est égal au montant emprunté,
€.
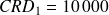Les intérêts de la période 1 sont
€.
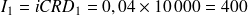L'annuité est
€.
L'amortissement de la période 1 est égal à l'annuité diminuée des intérêts de la période, soit
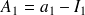, on a donc
€.
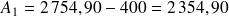Ligne 2 :
Le capital restant dû en début de période 2 est égal au capital restant dû au début de la période précédente, diminué de l'amortissement de la période précédente, soit
€.
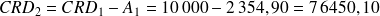Le restant de la ligne 2 est complété de la même façon qu'a été complétée la ligne 1, et ainsi de suite sur toutes les lignes de l'échéancier.
e) Remarques
• Sur la dernière ligne, l'amortissement est égal au capital restant dû en début de période.
• Si on calculait la somme des amortissements, celle-ci serait égale au montant emprunté.
Ces deux remarques permettront à l'avenir de vérifier que le tableau d'amortissement ne comporte pas d'erreur.
• Le coût de l'emprunt est égal à la somme des intérêts ou encore à la somme des annuités diminuée du montant de l'emprunt. Ici il est de
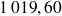€ et on peut vérifier que
€.
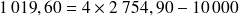