Approfondissements
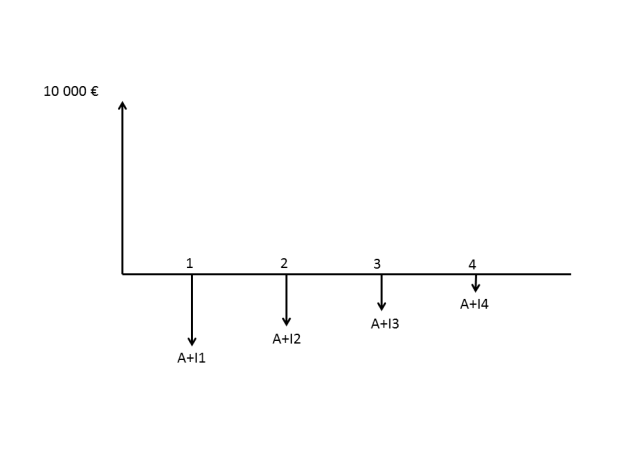
a) Diagramme des flux
Un emprunt de 10 000 € consenti au taux de 4% annuels doit être remboursé en 4 ans. L'amortissement du capital emprunté se fera par tranches égales.
Commentaire :
À chaque période, une même fraction du capital emprunté est amortie et les intérêts ainsi que les versements périodiques décroissent.
b) Valeur de chaque tranche d'amortissement
€
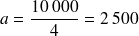Question
Le capital emprunté est amorti par tranches égales sur 4 ans, autrement dit un quart des
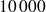€ empruntés soit
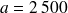€ sera remboursé chaque année.
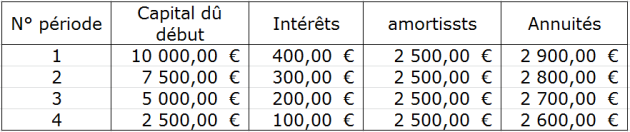
c) Tableau d'amortissement
D'une période à l'autre le capital restant dû se trouve diminué d'un même montant
de sorte que les intérêts ainsi que l'annuité diminuent.
Important :
Les annuités forment une suite arithmétique de raison
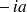et de premier terme
.
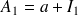On peut le vérifier : en diminuant l'annuité d'une période d'un montant
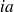soit ici de
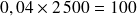€, on obtient l'annuité de la période suivante, et l'annuité de la première période est
€.
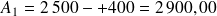Remarque :
Ce tableau comporte 5 colonnes (voir tableau d'amortissement par annuités constantes) et une ligne par année plus une ligne portant les intitulés de colonne, la colonne 1 comportant les numéros de période.
d) Construire le tableau d'amortissement
A vous de jouer !
Question
Comment construire le tableau d'amortissement ?
On doit utiliser les formules :
•
•
•
•
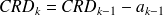
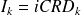
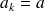
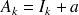
Ligne 1 :
Le capital restant dû en début de période 1 est égal au montant emprunté,
€.
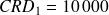Les intérêts de la période 1 sont
€.
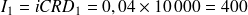L'amortissement est égal à
€.
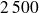L'annuité de la période 1 est
€.
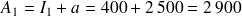Ligne 2 :
Le capital restant dû en début de période 2 est égal au capital restant dû au début de la période précédente, diminué de l'amortissement constant, soit
€.
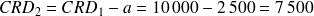Le restant de la ligne 2 est complété de la même façon qu'a été complétée la ligne 1 et ainsi de suite sur tout l'échéancier.
e) Remarques
Les trois remarques faites à l'issue de l'échéancier précédent restent valables :
• Sur la dernière ligne, l'amortissement est égal au capital restant dû en début de période.
• Si on calculait la somme des amortissements celle-ci serait égale au montant emprunté.
• Le coût de l'emprunt est égal à la somme des intérêts ou encore à la somme des annuités, diminuée du montant de l'emprunt. Ici il est de
€.
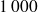