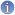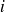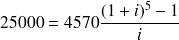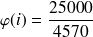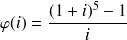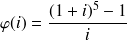Exemple
Voici l'exemple que nous allons traiter.
Nous nous situons dans le contexte d'un placement financier : il s'agit donc d'une opération de capitalisation.
Ici, ce sont des versements multiples, réguliers et constants.
Exemple :
La banque me garantit que je pourrai me constituer un capital de 25000 € en 5 ans, en déposant 4570 € chaque fin d'année sur le compte-épargne qu'elle me propose. Quel serait le taux de rémunération annuel de ce compte ? |
Voici le résultat dans le tableur :
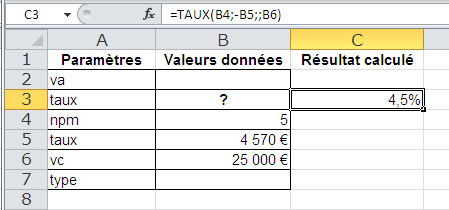
On utilise la fonction TAUX.
Solution : taux = 4,5%
Npm : 5 ans
Vpm = - 4570 € : montant des versements multiples, appelé avec un signe négatif car ce sont des décaissements.
Va = 0 (pas de dépôt initial)
Vc = 25000 €
Type = 0 et peut être omis.
Syntaxe : =TAUX(npm ; vpm ; va ; [vc] ; [type])
Appel de fonction : consulter la barre de formule dans l'image ci-dessus.
Appel équivalent: =TAUX(5;-4570;;25000)
Conseil :
A noter :
L'argument va est obligatoire, vous devez donc saisir la valeur 0.
Et vc est précédé d'un signe « + », c'est la valeur capitalisée associée.
Ainsi, la fonction TAUX comporte des flux de signes opposés.
Remarque :
Formule mathématique sous-jacente : Il s'agit de calculer le taux
Autrement dit,
Cette équation n'admet pas une solution qui pourrait s'exprimer simplement sous la forme
Cependant en remarquant que
Cette méthode est appelée "résolution par dichotomie[2]". |  |
On apprécie ici la facilité d'utilisation d'un tableur !
Sinon, il faudrait recourir aux tables financières ou utiliser une calculatrice financière.
Anecdotiquement, on peut également calculer le taux par l'une des méthodes de calcul par approximation disponibles : par dichotomie [2] ou par balayage[3].