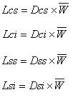Gestion des flux

Cours
Outils

Calcul des limites

Si l'on considère (à vérifier) que la moyenne des échantillons suit une loi normale alors 99,8% (99,74%) des mesures sont comprises dans l'intervalle moyenne ± 3,09(3) σx.

σx étant l'écart-type de la distribution des moyennes des échantillons.

schéma

On peut alors calculer les limites de contrôle de la carte :

(les limites de surveillance sont calculées de la même manière en ajoutant non pas trois mais deux écarts-type).

Calculons par exemple la limite de contrôle supérieure.

T étant la valeur cible.

Or relation donnée par les statisticiens.

étant l'écart-type de la population, n la taille de l'échantillon.

Or dans la majorité des cas est inconnue donc il faut l'estimer.

On peut l'estimer à partir de la moyenne des étendues ou de la moyenne des écarts-type des échantillons.

étant la moyenne des étendues et étant la moyenne des écarts-type

c4 et d2 des coefficients permettant l'estimation et variant en fonction de n sont donnés par les statistiques.

tableau

Calculer le coefficient A à placer devant la moyenne des étendues lorsque n= 5

Méthode :

formule

Ces coefficients permettant de calculer les limites se trouvent dans les tables suivantes.

Carte de contrôle de la moyenne (les deux premières tables)

1) cas m et (caractéristiques de la population) sont connus

limites de contrôle :

(table 1 première colonne)

limites de surveillance : (table 1 deuxième colonne)

2) cas estimé à partir de la moyenne des étendues :

limites de contrôle : (T valeur cible)

(table 2 première colonne)

limites de surveillance :(table 2 deuxième colonne)

3) cas estimé à partir de la moyenne des écarts-type :

limites de contrôle :

(table 3 première colonne)

limites de surveillance :(table 3 deuxième colonne)

table 1 - Table 2

Table 3

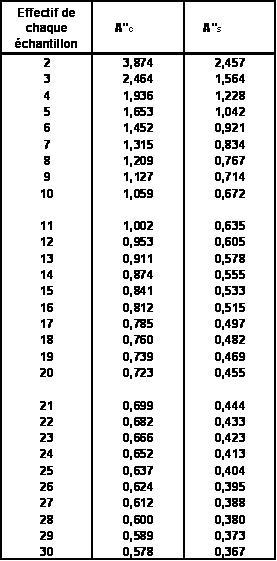
Carte de contrôle de l'étendue

Table 1 (sigma connu)

Table 1

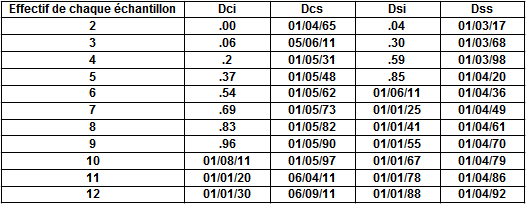
Table 2 (sigma estimé à partir de )

Table 2

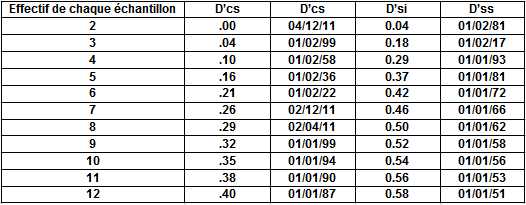
Cas où les caractéristiques de la population sont connues

Cas où les caractéristiques de la population sont inconnues et estimées à partir de la moyenne des étendues.

Calculer les limites de contrôle de la moyenne et de l'étendue :

Lors de la réalisation d'une pièce de longueur 10± 0,1 mm nous avons prélevé 25 échantillons de 5 pièces. Pour chaque échantillon a été calculé sa moyenne et son étendue. La moyenne des étendues de chaque échantillon est de 0,093 mm.

Calculer les limites de contrôle et de surveillance de la moyenne et de l'étendue.