L'algorithme de Johnson
Son objectif est de minimiser la durée de réalisation d'une file d'attente de n pièces devant toutes passer selon le même ordre sur deux machines (problème du type flow-shop).
Il peut s'énoncer ainsi :
Tant qu'il reste des pièces dans la file d'attente
Faire
Pour le reste des pièces à ordonnancer
Faire la recherche sur les deux machines
du temps opératoire minimum (TOM);
Si TOM est trouvé sur la première machine
alors placer la pièce en début d'ordonnancement;
sinon placer la pièce en fin d'ordonnancement;
fin de si
éliminer de la file d'attente la pièce nouvellement ordonnancée;
Fin de faire
Exemple :
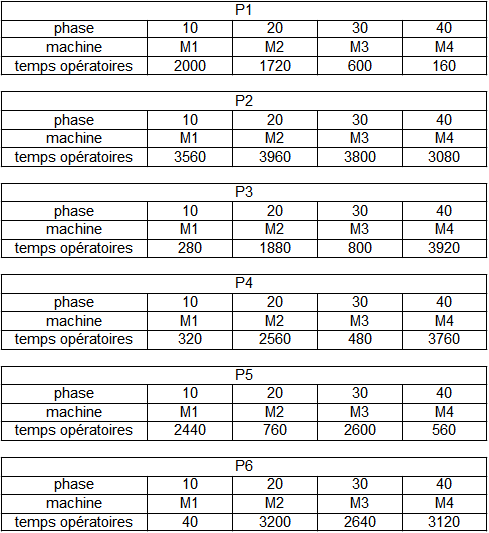
Considérons 4 pièces P1 P2 P3 et P4 qui vont passer successivement sur les machines M1 et M2 afin d'être fabriquées.
Les gammes de fabrications s'écrivent ainsi :
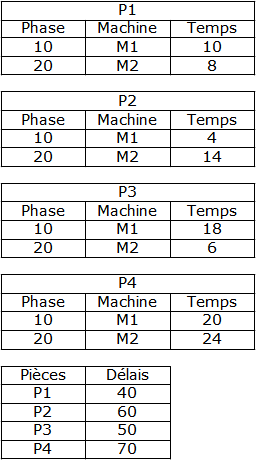
Appliquons l'algorithme de Johnson
Le TOM 4 nous permet de placer P2 en premier
Puis le TOM 6 P3 en dernier etc...
On obtient ainsi l'ordre suivant : P2, P4, P1, P3
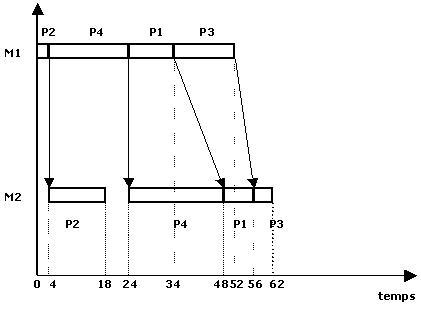
On constate qu'il ne reste qu'un seul trou de charge après P2 sur la machine M2 et que si cet algorithme minimise bien le temps global de fabrication il ne permet pas forcément de respecter les délais de réalisation spécifiques de certaines pièces.
Exemple :
P1 est terminée à 56 alors qu'elle a un délai de 40 et P3 à 62 avec un délai de 50.
Algorithme de Johnson généralisé
Il peut s'appliquer sur toute fabrication dont le processus de fabrication est séquentiel avec plus de deux postes de fabrication même si tous les postes ne sont pas utilisés.
Pour chaque pièce :
- Réaliser la somme des temps de toutes les phases (N)
- Réaliser la somme x des temps des n-1 premières phases
- Réaliser la somme y des temps des n-1 dernières phases
- Calculer le rapport k=x/y
On obtient l'ordre des fabrications grâce à l'ordre croissant de k.
Exemple :
Soit une file d'attente composée de six pièces et devant être fabriquées séquentiellement sur 4 machines, les temps opératoires sont exprimés en centièmes d'heures.
L'ordre de passage est donc : P3 P4 P6 P2 P5 P1
