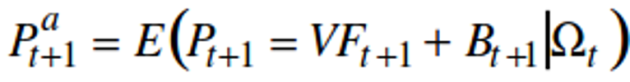Approfondissement : le modèle des bulles rationnelles
Les modèles de « bulles rationnelles » s'appuient sur cette construction autoréalisatrice des prix. Nous présenterons le cas simple de bulle déterministe exponentielle, proposée par Blanchard O.J. et Watson[1] M.W. [1982].
Méthode :
On suppose que le prix dépend de la valeur fondamentale (VFt) et d'une variable Bt, dont la loi est une suite géométrique de premier terme B0 (B0<0) et de raison (1+r), s'écrivant :
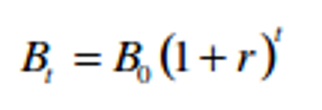
Avec Bt la bulle en t, B0 la bulle en 0 et r le taux d'intérêt supposé constant.
Les agents croient que le prix s'exprime à partir de la valeur fondamentale et d'un terme particulier, la bulle qui traduit l'opinion du marché.
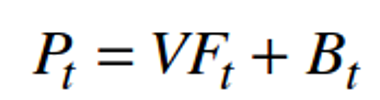
Avec Pt le prix à la date, VFt la valeur fondamentale en t et Bt la bulle en t.
Or, cette régularité a la particularité d'être autoréalisatrice. En effet, si l'on suppose que les agents ont des anticipations rationnelles, leurs anticipations s'écriront :
Avec Pat+1 l'anticipation du prix en t pour t+1, Pt+1 le prix en t, VFt+1 la valeur fondamentale en t+1, Bt+1 la bulle en t+1 et Ωt l'ensemble des informations détenues en t.
Comme l'espérance conditionnelle de Bt s'écrit :
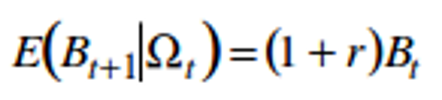
Le prix anticipé par les agents s'écrit finalement :
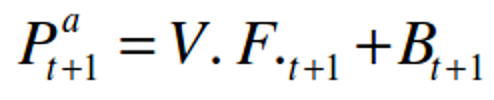
On observe que cette anticipation est conforme à la loi du prix. Dans la mesure où ces anticipations déterminent l'action des individus, le prix réalisé s'établira suivant cette régularité. La prophétie est autoréalisatrice.
Remarque :
Le modèle des bulles rationnelles montre comment les agents ont intérêt à fonder leurs anticipations de prix sur l'opinion du marché puisque le prix se conforme effectivement à cette règle. Le prix s'éloigne durablement alors de la valeur fondamentale.
Remarque :
Ce modèle simple ne permet pas d'expliquer la survenance d'un changement d'opinion : une fois qu'une dynamique (à la hausse ou à la baisse) est engagée, elle perdure dans la même direction, éloignant toujours plus le prix de sa valeur fondamentale.
Pour corriger cet effet, il faut introduire un facteur aléatoire comme des chocs de liquidité ou la présence d'acteurs irrationnels. Ce dernier cas est qualifié de bulles irrationnelles.
Pour aller plus loin, Artus P.[2] [1995], Anomalies sur les marchés financier.