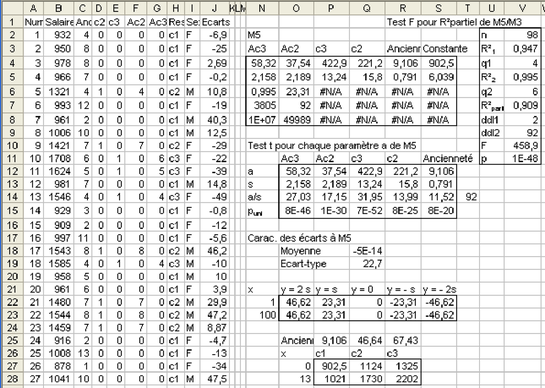
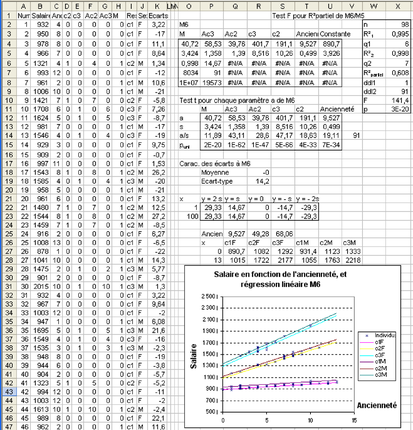
Modèle 5 : La régression linéaire multiple avec interaction entre 2 variables
On repart de M3, et on essaie de l'améliorer par la prise en compte d'autres effets. On désire prendre en compte une augmentation annuelle de salaire différente selon les responsabilités. Cela s'appelle une interaction entre la variable responsabilité et la variable ancienneté. Pour cela on ajoute la variable produit des deux, donc deux colonnes supplémentaires, Ac2 et Ac3, qu'on obtient par produits respectifs des colonnes A et c2, A et c3), ce qui donne S = a1 A + a2 c2 + a3 c3 + a4 A c2 + a5 A c3 + b + e (on dit encore que le modèle est linéaire car il est une combinaison linéaire des paramètres à estimer a1, a2, ..., a5, b, mais certains auteurs ne disent plus régression linéaire dans ce cas, comme dans le cas où des variables sont élevées à une puissance quelconque).
Question
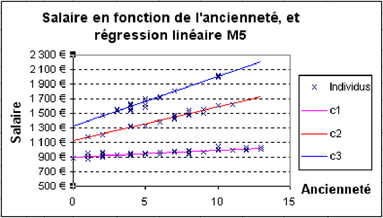
Q1. Ajouter ces deux variables dans des colonnes et estimer le modèle, et tester son apport par rapport à M3. Donner l'équation générale du modèle, ainsi que les équations par responsabilité. Puis représenter graphiquement le nuage de points ainsi que les 3 droites de régression du salaire sur l'ancienneté pour chaque responsabilité (voir figure 5.38).
Question
Q2. Tester le modèle M5 par rapport au modèle M4. Ainsi que les paramètres du modèle. Représenter les résidus en fonction du sexe. On voit que cette fois la différence est bien visible entre les résidus des 2 sexes. Il faut donc essayer à nouveau de faire entrer le sexe dans le modèle. Écrire le modèle M6 et le tester.