Traitement de données avec tableur appliqué à l'Economie et la Gestion.

Modèle 3 : La régression linéaire multiple à deux variables mixtes

Question

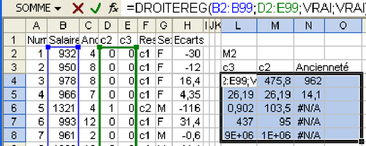
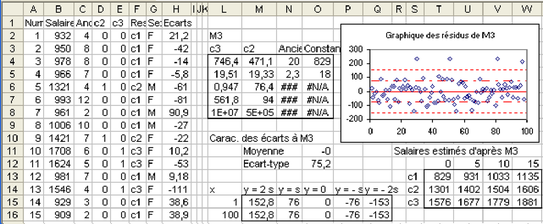
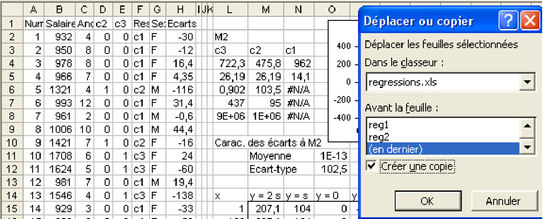
Q1. Faire une copie de la feuille de calcul (voir Figure 5.32), puis corriger afin de prendre dans les variables explicatives à la fois l'ancienneté et la responsabilité. Écrire l'équation du modèle M3 trouvé puis faire un tableau donnant les estimations de salaires pour 12 personnes, dont l'ancienneté prend les valeurs 0, 5, 10, 15 et les 3 responsabilités c1, c2 et c3.

Figure 5.32 : copie de la feuille de calcul contenant le modèle M2 pour la corriger en un modèle M3 sous Excel

Solution

Question

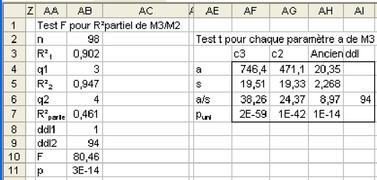
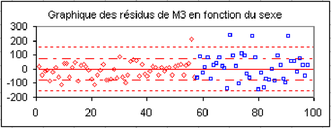
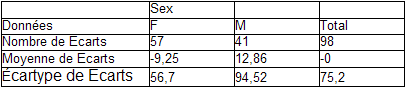
Q2. Le modèle M3 est-il bien meilleur que le modèle M2 ? Pour tester la significativité de l'augmentation de R², c'est-à-dire le fait que cette augmentation n'est pas due au hasard, plusieurs méthodes existent dans le cas de modèles emboîtés, la plus ancienne étant de calculer la statistique R²partiel/(1-R²partiel)/(q2-q1)*(n-q2) avec R²partiel=(R²2-R²1)/(1-R²1), où R1 et R2 sont les coefficients de détermination respectifs de M2 et M3, qui doit suivre la loi de Fisher Snedecor (appelée loi.F dans les fonctions du tableur), à (q2-q1) et (n-q2) degrés de liberté, q1 et q2 étant le nombre de paramètres respectifs de M2 et M3, soit ici 3 et 4. Quelle est votre conclusion ? Examiner les résidus, seuls, puis groupés par sexe. A votre avis la variable sexe doit-elle être mise dans le modèle ?

Solution

le R² est passé de 0,906 à 0,947, ce qui indique une amélioration, mais elle n'a pas nécessairement de sens. En effet chaque fois qu'on ajoute une variable, la valeur de R² augmente généralement, au point que si on met autant ou plus de variables que d'individus, on peut obtenir un R² de 1. Il faut contrôler que l'augmentation de R² a un sens (du point de vue statistique). Nous avons proposé d'utiliser pour cela la statistique F=R²partiel/(1-R²partiel)/(q2-q1)*(n-q2) avec R²partiel=(R²2-R²1)/(1-R²1), on peut voir les résultats du calcul dans la cellule AB10, et la probabilité p d'avoir un R²partiel aussi grand par hasard est inférieure à 0,01, ce qui nous permet de conclure que le R²partiel est très significatif, et que le passage du modèle M2 au modèle M3 est justifié statistiquement.

pour trouver exactement les mêmes valeurs que dans la figure 5.35, il faut veiller à écrire dans les formules les adresses des nombres si ceux-ci ne sont pas entiers, et non les valeurs qu'on voit à l'affichage, car ce sont leurs valeurs approchées (par exemple dans la cellule AB3 la formule est =reg2!L6). La valeur de p se trouve par la formule LOI.F(AB10;AB8;AB9) écrite dans AB11.

On peut aussi tester la significativité de chaque paramètre du modèle (c.à.d. qu'ils diffèrent significativement de 0). Le test peut être bilatéral (on ne sait pas s'ils risquent d'avoir un effet positif ou négatif sur le salaire), ou unilatéral. Ici on suppose que l'ancienneté, la responsabilité élevée ont un effet positif sur le salaire, c'est un test unilatéral. Pour calculer la statistique t = a/s, on utilise les deux premières lignes du modèle de régression. On sait que si t dépasse largement 2, et que le ddl est élevé, comme ici, la probabilité p d'avoir une valeur si grande par hasard sera très faible. Elle est calculée dans la ligne 7. Dans la cellule AF7 on a la formule =LOI.STUDENT(AF6;$AI6;1) qu'on recopie vers la droite. On obtient que toutes les valeurs de p sont inférieures à 0,01 et donc que les 3 paramètres sont très significatifs. Il est à noter que le passage de M2 à M3 porte sur une seule variable, la variable ancienneté, et comme elle est unique, on a la relation entre la valeur tancienneté et FM3/M2 : t²=F. Et quand on prend un test bilatéral, ce qui n'est pas le cas ici, on trouve la même probabilité avec t ou avec F. Avec un test unilatéral, on trouve une probabilité associée à F double de celle associée à t.

Figure 5.35 : Réalisation du test de significativité du modèle M3/M2 à gauche et de tous les coefficients de l'équation de régression de M3 à droite. Tout est très significatif, les valeurs de p étant <0,01

Le calcul des résidus doit être aussi mis à jour. La formule dans H2 est =B2-O$4-M$4*D2-L$4*E2-C2*N$4 et on la recopie vers le bas. A ce moment-là, dans les caractéristiques des résidus, la moyenne passe à 0 et l'écart-type devient peu différent du contenu de la cellule. Les équations des 5 droites sont mises à jour et le graphique des résidus également. Si on fait le graphique des résidus en fonction du sexe, on voit que les résidus des femmes (losanges rouges) sont plus groupés autour de l'axe que ceux des hommes (carrés bleus)., ce qui montre une différence de variance.

Figure 5.36: Les résidus de M3 diffèrent selon le sexe

On vérifie cela par un tableau croisé dynamique donnant les statistiques des écarts. On constate alors que non seulement les variances (ecart-type²) diffèrent mais également les moyennes. Ce qui invite à prendre en compte le sexe dans le modèle.

Tableau 1

Modèle 4 : La régression linéaire multiple avec 2 variables qualitatives et une quantitative (page suivante)Modèle 2 : La régression linéaire à variables qualitatives (page Précédente)

Accueil Pôle de Recherche et d'Enseignement Supérieur de l'Université de Lorraine