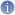La prise de décision risquée
Dans un univers certain ou de certitude, les économistes supposent que les individus maximisent une fonction d'utilité[1] qui porte sur l'espace des biens matériels. |  |
Complément :
Dans un univers d'incertitude, cependant, les biens ne sont pas toujours disponibles. Leur disponibilité dépend d'états de la nature qui se réalisent ou non, comme, par exemple, du temps qu'il fera pour les biens alimentaires.
Lorsqu'il est possible d'assigner une probabilité d'occurrence à ces états de la nature, la décision est dite risquée.
Prenons un exemple.
Imaginez que l'on vous propose de jouer à la loterie suivante :
vous avez une chance sur deux de gagner 100 euros ;
et une chance sur deux de ne rien gagner du tout.
Combien êtes-vous prêt à donner pour jouer à cette loterie ? 50 euros ? 30 euros ou seulement 15 ?
Comme la plupart des gens, vous avez dû répondre 30 ou 15 et non 50, ce qui veut dire que votre décision optimale ne correspond pas à l'espérance de gain (égale à 50) mais à l'espérance d'une fonction de ce gain.
Pourquoi cela ?
Tout simplement parce que l'espérance de gain ne prend pas en compte l'aversion au risque caractéristique de la plupart des individus. Si vous n'aviez aucune aversion au risque, vous auriez en effet choisi de miser 50 euros.
Pour prendre en compte cette aversion, on suppose donc, à la suite des travaux de Daniel Bernouilli (1700-1782), que les individus maximisent la fonction d'espérance d'utilité (EU) de la loterie qui correspond à l'espérance mathématique de l'utilité des conséquences :
EU(Loterie) = 0,5 * U(100) + 0,5 * U(0).
Fondamental :
On en déduit le critère de choix en univers risqué : une loterie L1 sera préférée à une autre loterie L2 si et seulement si EU(“L1”) > EU(“L2”).
Tout l'argumentaire des économistes est alors de considérer que l'on peut raisonner à partir d'un espace sur les loteries (risquées) aussi aisément qu'avec des paniers de biens.
Les paradoxes d'Allais (1953) et celui d'Ellsberg (1961) montrent cependant que ce n'est pas le cas.