EXERCICE 1
Soient trois fonctions d’utilité :
Ua (x , y) = 3x1/3 . 4y1/2
Ub (x , y) = 6x3 + 7y2
Uc (x , y) = 2x . y2 + 3y
Question
1. Le TMS dans chacun des cas est-il croissant, décroissant ou constant par rapport à x ?
Le TMS est décroissant pour Ua.
Uc est croissant pour Ub.
Question
2. Les courbes d’indifférence associées respectivement à Ua, Ub et Uc sont-elles convexes par rapport à l’origine ?
Les courbes d'indifférence associées à Ua et Uc sont convexes.
EXERCICE 2
Un consommateur procède au classement suivant entre 6 paniers de deux biens X et Y :
Il préfère strictement le panier (8 ; 48) au panier (15 ; 15).
Il est indifférent entre (15 ; 10) et (3 ; 12).
Il préfère strictement le panier (15 ; 15) au panier (10 ; 45).
Il préfère strictement le panier (10 ; 45) au panier (9 ; 48).
Question
Peut-on considérer que le classement de ce consommateur est rationnel ? Argumentez votre réponse.
Le panier (8 ; 48) est préféré au panier (15 ; 15) et le panier (15 ; 15) est préféré au panier (10 ; 45).
D'après l'axiome de transitivité, le panier (8 ; 48) est donc préféré au panier (10 ; 45).
Or, le panier (10 ; 45) est préféré au panier (9 ; 48).
Donc, si l'agent est rationnel, on doit avoir (8 ; 48) préféré à (9 ; 48) !
Ce qui n'est pas possible si on suppose que les agents préfèrent toujours avoir plus que moins !
EXERCICE 3
EPO et Anabolisants, les managers et médecins d'une équipe cycliste, souhaitent que leurs coureurs soient musclés (on associera le muscle au poids), rapides et obéissants. Ils préfèrent un coureur A à un coureur B lorsque A est supérieur pour 2 des 3 caractéristiques au moins, sinon, ils sont indifférents entre A et B.
Richard pèse 80 kg, pédale à une vitesse moyenne de 30km/h et accepte 4 piqûres par semaine.
Laurent pèse 75 kg, pédale à une vitesse moyenne de 50km/h et accepte 2 piqûres par semaine.
Alex pèse 70 kg, pédale à une vitesse moyenne de 40km/h et accepte 8 piqûres par semaine.
Question
1. Comment EPO et Anabolisants classent-ils les coureurs deux à deux ? Qu'en conclure sur leur relation de préférences ?
Les préférences ne sont pas transitives. En effet, Richard est préféré à Laurent et Alex est préféré à Richard mais Laurent est préféré à Alex.
Question
2. Après plusieurs saisons d'échecs, les managers modifient leur manière d'évaluer les coureurs : ils préfèrent un coureur à un autre lorsqu'il est meilleur sur les 3 critères et sont indifférents lorsque les caractéristiques sont identiques. Dans les autres cas, ils estiment qu'ils ne peuvent pas comparer. Que dire de cette nouvelle relation de préférences à partir des hypothèses de comportement ?
On ne peut pas comparer les 3 coureurs, les préférences sont incomplètes.
EXERCICE 4
La fonction d'utilité du Petit Nicolas pour les glaces au chocolat (bien en quantité x) et pour les glaces à la fraise (bien en quantité y) est donnée par : UN (x,y) = x ½ y½ .
Question
1. Écrire l'équation de la courbe d'indifférence du Petit Nicolas associée à un niveau d'utilité u0 = 2
Les quantités de biens x et y située sur cette courbe d'indifférence doivent vérifier U(x,y) = 2 ou x(1/2) y(1/2) = 2
Pour donner l'équation de cette courbe d'indifférence dans le plan (x,y), il faut isoler y ce qui donne y=4/x. La courbe d'indifférence est donc une hyperbole.
Question
2. Construire cette courbe d'indifférence dans le plan (x,y)
La courbe d'indifférence y=4/x est donc une hyperbole. Elle passe par les points (1, 4), (2, 2), (4, 1).
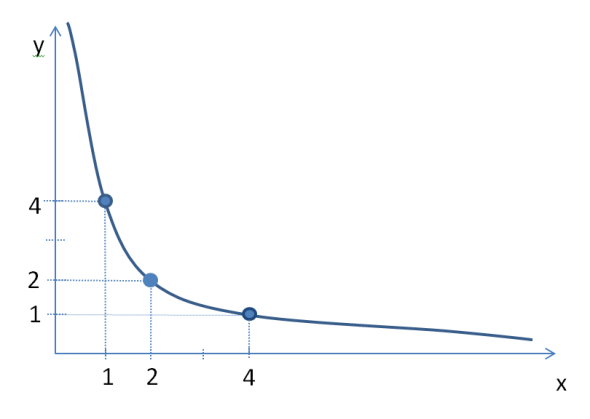
Question
3. Calculer le Taux Marginal de Substitution associé à 1 glace au chocolat et 4 glaces à la fraise à partir de l'équation de la courbe d'indifférence de 1.
Le TMS est égal à la valeur absolue de la pente de la tangente à une courbe d'indifférence : TMS = -dy/dx. Il peut être calculé, pour un panier d'une courbe d'indifférence d'équation y = f(x) à partir de f'(x).
Dans cet exercice, f(x) = 4/x, donc f ‘(x) = -4/x2 .
Pour les paniers de cette courbe d'indifférence, TMS = -dy/dx = 4/x2 .
On a donc TMS(1, 4) = 4
Question
4. Calculer le Taux Marginal de Substitution associé à 4 glaces au chocolat et 1 glace à la fraise. Comparez les deux TMS. Que pouvez-vous en déduire ?
En utilisant 3, on obtient TMS(4, 1) = ¼.
En comparant avec le TMS calculé en 3., on retrouve bien la propriété de décroissance du TMS : il diminue lorsque le nombre de glaces au chocolat dans le panier augmente.
Question
5. Calculez les utilités marginales des deux biens pour des quantités de biens x et y quelconques.
Par définition, Umx(x,y) = U'x(x,y) et Umy(x,y) = U'y(x,y)
Pour UN (x,y) = x ½ y½, on a Umx(x,y) = 1/2 x-1/2y1/2 et Umy(x,y) = 1/2 x1/2 y-1/2
Question
6. En déduire le Taux Marginal de Substitution entre les deux biens pour un panier sur une courbe d'indifférence quelconque.
TMS = -dy/dx = Umx(x,y)/(Umy(x,y) = y/x.
On peut vérifier qu'on retrouve, pour les paniers (1, 4) et (4,1) les mêmes TMS que dans 3. et 4.





