(suite)
Exercice 3
Soit un consommateur dont on représente la relation de préférence par la fonction d'utilité suivante : U(x , y) = 3x + 4y où x et y indiquent les quantités de bien 1 et de bien 2.
Question
1. Représenter les 3 courbes d'indifférence correspondant à des niveaux d'utilité de 30, 40 et 50.
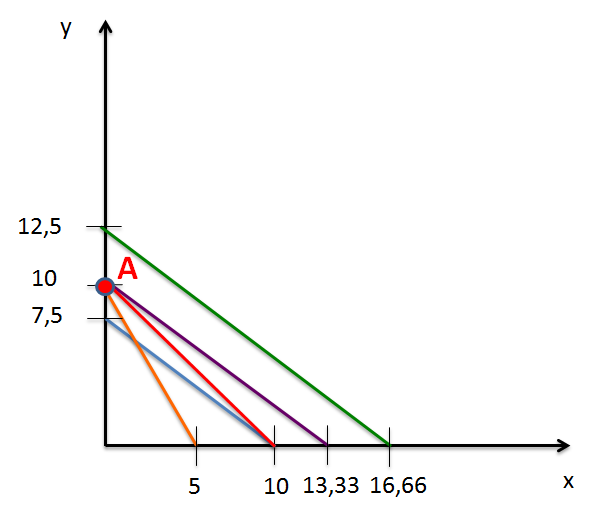
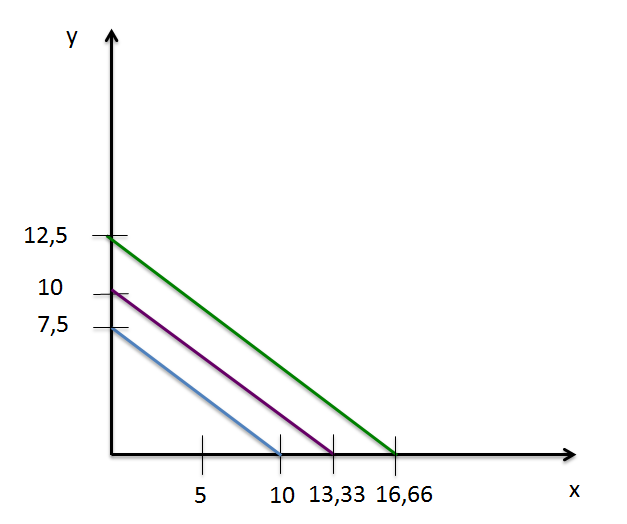
Utilité de 30 : 30 = 3x + 4y soit l'équation dans le plan (x,y) de la fonction y = 7,5-(3/4)x. Courbe d'indifférence représentée en bleu.
Utilité de 40 : 40 = 3x + 4y soit l'équation dans le plan (x,y) de la fonction y = 10-(3/4)x. Courbe d'indifférence représentée en violet.
Utilité de 50 : 50 = 3x + 4y soit l'équation dans le plan (x,y) de la fonction y = 12,5-(3/4)x. Courbe d'indifférence représentée en vert.
Question
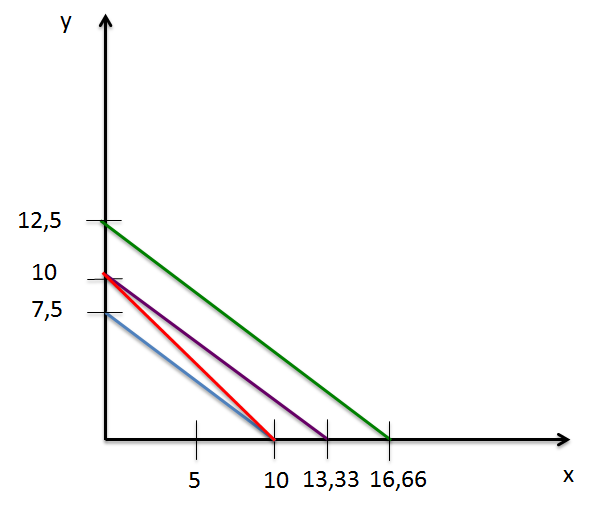
2. En supposant que le revenu R de ce consommateur est de 10 et les prix des deux biens sont égaux à 1, représenter la contrainte de budget sur le même graphique.
L'équation de la droite de budget est x + y = 10. Elle est représentée en rouge sur le graphique.
Question
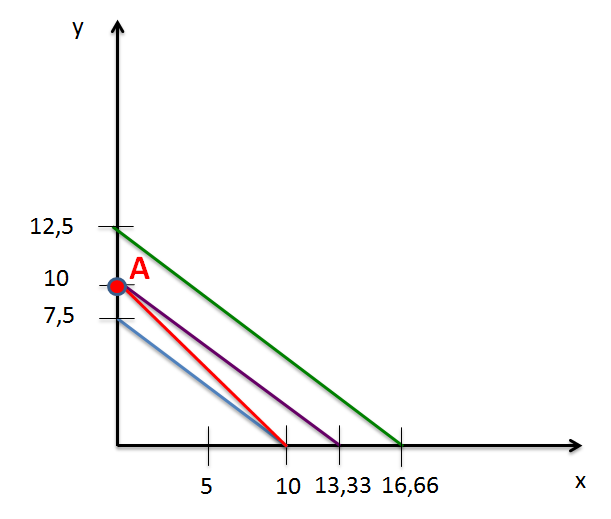
3. Quel est le panier de bien optimal ?
Le panier de bien optimal permet d'atteindre la plus grande satisfaction (courbe d'indifférence la plus éloignée de l'origine) tout en tenant compte de la contrainte de budget. C'est donc le panier représenté par le point A sur la courbe d'indifférence en violet et sur la droite de budget en rouge. Il s'agit du panier qui contient 10 unités de bien 2 et 0 de bien 1.
Question
4. Que se passe-t-il si le prix du bien x augmente et passe de 1 euro à 2 euros ?
L'équation de la droite de budget devient : 2x + y = 10. Elle est représentée en orange. Cela ne change pas le panier optimal.