Cours (suite)

3 graphe sagital

32 Pert potentiel tâches

Nous allons établir le graphe sagital pour le Pert potentiel tâches . Dans cette représentation les tâches sont représentées aux sommets(potentiels) du réseau.

Les vecteurs liant les sommets et toujours orientés dans le sens du défilement du temps représentent pour leur part les relations de dépendance existant entre les tâches.

Reprenons l'exemple précédent :

Nous pouvons conserver la répartition par niveaux établie grâce à la matrice des antériorités.

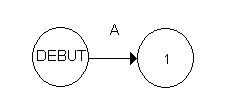
Nous débutons le graphe avec les tâches de premier niveau ici la tâche A.

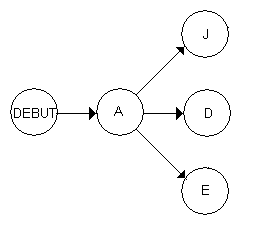
Les trois tâches D,E et J sont de niveau deux et ont pour antécédent la tâche A, elles vont donc débuter en parallèle juste après A.

Les trois tâches B,C et F sont de niveau trois sachant que B et C ont pour antécédent E et que F a pour antécédent D et E.