Traitement de données avec tableur appliqué à l'Economie et la Gestion.
CoursOutils transverses

Exercice TD

Question

1 :

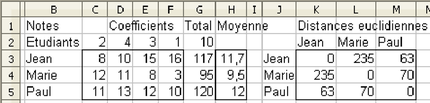
On donne les coefficients de 4 épreuves (Fig 3.23, cellules C2 à F2) composant un examen et les notes de 3 étudiants à ces épreuves (C3 à F5). Utiliser des fonctions matricielles de type « somme » pour trouver pour chaque étudiant 1) sa moyenne pondérée à l'examen (colonne H), 2) sa distance euclidienne aux autres étudiants (cellules K3 à M3). Trouver les formules matricielles permettant de lier les intitulés de ligne et de colonnes du tableau de distances euclidiennes aux 3 noms saisis en colonne B.

Figure 3.23 : Calculs illustrant l'utilisation de fonctions matricielles de type « somme »
Figure 3.23 : Calculs illustrant l'utilisation de fonctions matricielles de type « somme »
Solution

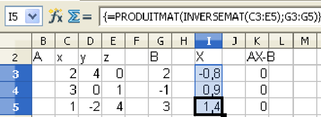
Question

2 :

Résolution d'un système de n équations à n inconnues. : On le met sous de produit matriciel AX=B, et la solution, si elle existe et est unique, est donnée par X=A-1B. Résoudre le système de 3 équations 2x + 4y = 2; 3x + z = -1 ; x – 2y + 4z = 3. Une fois trouvée la valeur de la matrice X, calculer AX-B qui doit être nul.

Solution
Exercices appliqués à l'économie avec correction (page suivante)Opérateurs et fonctions matricielles (page Précédente)
Accueil Pôle de Recherche et d'Enseignement Supérieur de l'Université de Lorraine Réalisé avec SCENARI