Opérateurs et fonctions matricielles
Les opérateurs arithmétiques fonctionnent aussi avec des matrices de même taille, et rendent les matrices obtenues en appliquant les opérateurs termes à termes (Fig. 3.21). Pour les utiliser on procède comme indiqué dans le paragraphe précédent pour l'addition de deux matrices (Fig. 3.20). Plus généralement, on peut aussi appliquer des fonctions numériques à une matrice (comme « sin ») et obtenir une matrice ayant comme termes les sinus des termes de la matrice d'origine.

On peut également utiliser les opérateurs arithmétiques de façon mixte, c'est-à-dire en mêlant scalaires et matrices dans les opérations. On obtient dans la plupart des cas des matrices alors que l'écriture des formules n'est pas toujours en adéquation avec les normes mathématiques usuelles (Fig. 3.22).
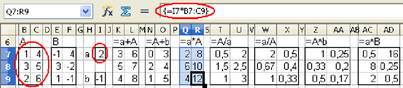
On dispose d'un « vrai » calcul matriciel (selon les normes mathématiques) sous forme de fonctions, dont les plus intéressantes sont les trois premières du tableau ci-dessous, car elle permettent de réaliser en quelques clics des calculs qui peuvent être longs et complexes. Les autres fonctions du tableau sont plutôt utilisées pour les calculs statistiques.
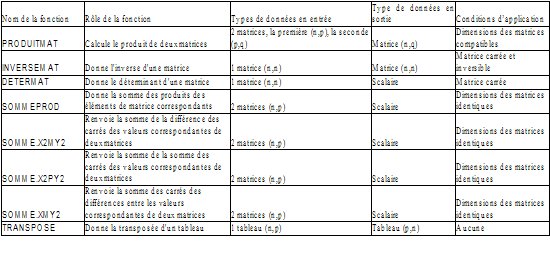
À ces fonctions, s'ajoutent les fonctions de « classeur » qui permettent de chercher des informations dans la matrice ou dans le tableau de nombres. Par exemple la fonction INDEX, qui utilise des coordonnées pour trouver une valeur à l'intérieur d'un tableau, s'utilise quand on veut accéder de façon plus individuelle aux cellules d'un tableau, la fonction RECHERCHE permet de « recoder » en remplaçant les valeurs présentes dans une colonne (resp. ligne) par les valeurs correspondantes présentes dans une autre colonne (resp. ligne), ces dernières, numériques ou textuelles, devant être rangées dans l'ordre croissant.
