Combinaison de plusieurs opérateurs dans une même expression

Il est courant d'écrire plus d'un opérateur arithmétique au sein d'une même expression. Quand c'est le même opérateur qui est utilisé plusieurs fois, le calcul se fait par étapes successives de la gauche vers la droite : pour calculer par exemple 2-3-4, on calcule d'abord 2-3, qui fait -1, puis -1-4, qui fait -5. Quand il y a des opérateurs arithmétiques différents, il faut commencer par celui qui a l'ordre de priorité le plus élevé. Cet ordre diffère selon les langages. Pour la quasi-totalité de ceux-ci, la multiplication et la division ont un ordre de priorité plus élevé que l'addition et la soustraction et l'exponentiation a un ordre plus élevé que la multiplication et la division. Dans la plupart des calculatrices, le moins unaire à la même priorité que la soustraction, alors que dans les deux versions de tableurs que nous avons examinées (OpenOffice 3.1 et Excel 2003), il a une priorité plus élevée que l'exponentiation, et donc que la multiplication, la division, l'addition et la soustraction. Si on désire imposer un ordre particulier, on le fait en ajoutant des parenthèses à l'endroit approprié.

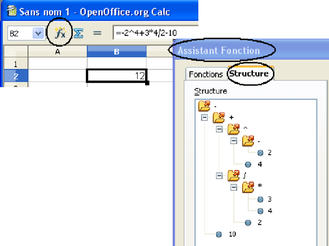
Calculons par exemple l'expression arithmétique -2^4+3*4/2-10 comme le tableur le ferait : Pour indiquer l'ordre des opérations, on met d'abord des parenthèses par ordre de priorité décroissante.

= -2^4+3*4/2-10

= (-2)^4+3*4/2-10 (- unaire)

= ((-2)^4)+3*4/2-10 (exponentiation)

= ((-2)^4)+((3*4)/2)-10 (* et /)

= (((-2)^4)+((3*4)/2))-10 (+ et -)

Puis on effectue les calculs en allant des parenthèses les plus internes aux plus externes.

= ( 16 +((3*4)/2))-10

= ( 16 +( 12 /2))-10

= ( 16 + 6 )-10

= 22 -10

= 12

On obtient ainsi 12 alors qu'on aurait obtenu -20 en effectuant ce calcul avec une calculatrice scientifique ordinaire. On peut voir dans la figure 3.7 une autre façon de représenter l'ordre des opérations. Cette notation appelée « notation polonaise », nationalité de son inventeur Jan Łukasiewicz, permet une écriture « préfixée des opérations, utilisée dans certains langages informatiques (Lisp) et calculatrices : l'opérateur est avant ses opérandes et non entre eux comme dans la notation classique appelée aussi « infixée ».

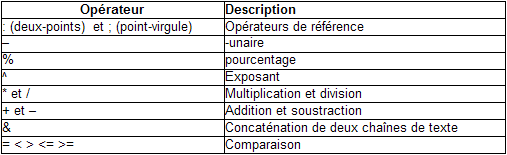
Le calcul d'une expression comportant des opérateurs de divers types se fait sur le même principe que celle comportant plusieurs opérateurs arithmétiques : en suivant l'ordre de priorité s'il n'y a pas de parenthèses, et en tenant compte d'abord des parenthèses s'il y en a. Toutefois mélanger des opérateurs de quatre catégories différentes définies précédemment a rarement du sens. Dans le tableau 3.1 figure l'ordre de priorité des opérateurs d'Excel.