Proposition 2
Le banquier propose maintenant à l'emprunteur de rembourser chaque fin de mois une même somme
, le taux annuel et la durée totale de remboursement restant les mêmes que ceux de la proposition 1, le diagramme ci-dessous illustre cette situation
Remarque :
La période de référence étant le mois, le nombre d'annuités versées est
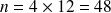et le taux utilisé doit être un taux mensuel, par exemple proportionnel, et sa valeur est alors :
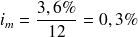.Dans le contexte de ce chapitre, les flux
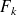sont les remboursements périodiques notés
.
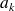Cliquez sur le bouton "lecture" pour lancer l'animation.
Calcul
€
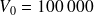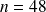
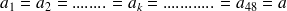
Le taux d'intérêt mensuel
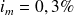réalise l'équilibre du diagramme de flux précédent soit :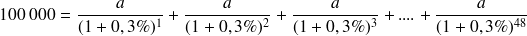
Ce qu'on peut également écrire, en utilisant les formules du chapitre 1, sous la forme :
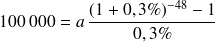
On en déduit la mensualité
€
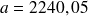En appui de son offre, l'établissement financier fournit un tableau d'amortissement dit échéancier qui résume le détail des remboursements et qui est construit ligne par ligne comme dans la proposition 1
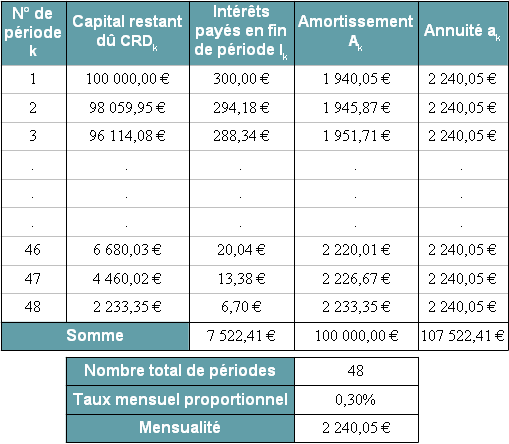
Remarque :
La somme des annuités diminuées du montant emprunté soit
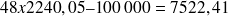€ représente le coût non actualisé du crédit. La somme des amortissements est égale au montant de l'emprunt.
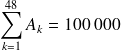
On peut remarquer que :
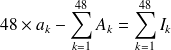autrement dit le coût non actualisé du crédit est égal à la somme des intérêts versés.
Remarque :
Alors que dans les deux propositions faites par la banque, le taux d'intérêt annuel est le même, le coût du crédit est plus élevé dans la proposition 1 que dans la proposition 2. Pour expliquer cela il faut entrer dans le détail des remboursements.
