Exercice TD 3
1) Résoudre de façon approchée l'équation x3-5x2+4x+1=0 1)
On doit déjà avoir une idée du nombre de solutions avant d'en rechercher des valeurs approchées. On sait que c'est le nombre de fois que la courbe d'équation y = x3-5x2+4x+1 rencontre l'axe des x. Pour dessiner cette courbe, écrire dans la colonne A à partir de la ligne 3 une suite de nombres de valeur initiale -1 et de raison 0,1. Puis dans B3 la formule « =A3^3-5*A3^2+4*A3+1 » ou « =A3*A3*A3-5*A3*A3+4*A3+1 ». Et « tirer » vers le bas afin de la recopier tant qu'il y a des valeurs dans la colonne A. Sélectionner ce bloc de valeurs x et y et insérer un graphique (nuage de points pour Excel, diagrammeXY pour OpenOffice).
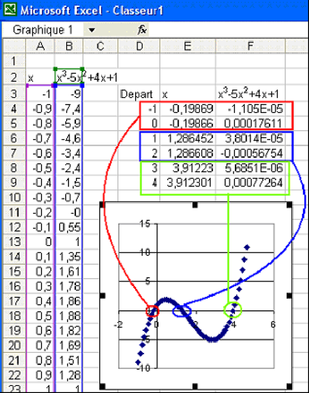
On a entouré les 3 points où la courbe rencontre l'axe des x : en rouge pour x entre -1 et 0, en bleu pour x entre 1 et 2, en vert pour x entre 3 et 4.
2) On écrit en E4 la valeur -1, et on fait un copier-coller de B3 vers F4. Puis on sélectionne F4 et on appelle l'outil « valeur cible ». La solution approchée apparaît dans la cellule E4 et remplace -1. Elle produit une valeur de F4 presque nulle. Comme -1 a disparu, on l'écrit dans la cellule D4 pour garder trace de la valeur dont est partie le tableur pour la recherche de solution.
3) On tape 0, 1, etc. sous la cellule D4, on les recopie sous la cellule E4, et on fait une copie de la formule de F4 dans les cellules du dessous. Puis on appelle l'outil « valeur cible » sur ces 5 cellules. On peut observer qu'on trouve à chaque fois une valeur approchée de la solution la plus proche de la valeur de départ.
