Le solveur

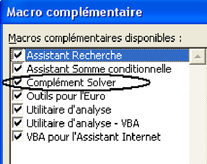
Il figure dans le menu « Outils » de la plupart des versions actuelles du tableur. Toutefois, s'il ne figure pas dans ce menu sous Excel, il est possible de le faire apparaître en allant dans « Outils>Macro complémentaire », et en cochant la case du solveur (Voir Fig. 4.27), puis en validant l'installation de cet outil. Le solveur est alors ajouté dans le menu « Outils ».

Étant donnée une fonction d'une ou plusieurs variables, le solveur a pour but de trouver des valeurs de ces variables qui rendent la fonction maximale, minimale, ou égale à une valeur donnée, dans un domaine particulier des variables, défini par des contraintes (inéquations, équations, valeurs entières). Comme pour la valeur cible, le solveur ne peut fournir qu'une solution, la plus proche des valeurs des variables utilisées pour écrire le problème.

Un problème simple pour débuter

Reprenons avec le solveur le problème traité dans la figure 4.25 avec l'outil « Valeur cible ». Pour cela on sélectionne la cellule H27, puis on appelle le solveur par « Outils>Solver »,

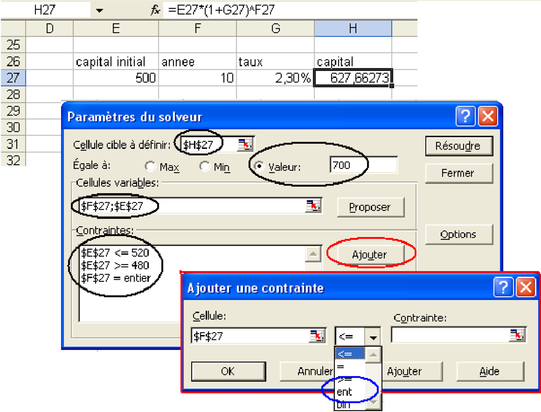
On a indiqué dans la figure 4.27 les paramètres du solveur à fixer. Pour cela, on se place dans la zone de saisie et on clique sur la cellule nécessaire et son adresse est recopiée dans la ligne de saisie. Tour en haut, l'adresse de la cellule cible est proposée, car on l'avait sélectionnée. On doit alors cocher la case « valeur » et taper le nombre 700 à côté de cette case. On peut maintenant choisir plus d'une cellule variable. Celle qui nous intéresse est la cellule F27 qui contient le nombre d'années. Une fois cette adresse écrite, on tape un « ; » et on clique sur la cellule E27 contenant le capital. En effet, bien qu'on ne désire changer que le nombre d'années, comme on souhaite qu'il soit entier, on autorise une petite modification du capital initial, sans laquelle le solveur signale qu'il ne peut pas trouver de solution. On ajoute alors une à une les contraintes. Le capital est autorisé à varier entre 480 et 520, et le nombre d'années doit être entier.

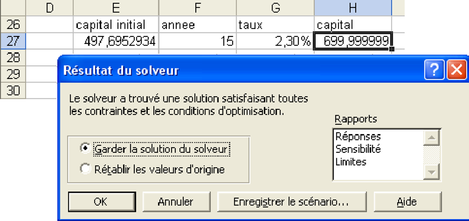
On enfonce alors le bouton « résoudre ». Une solution est proposée (voir Fig. 4.29), et si on choisit de la garder on retrouve bien les 15 ans d'intérêts pour que le capital obtenu soit de 700.

Un problème d'optimisation simple : la programmation linéaire

Les problèmes d'optimisation que peut résoudre le solveur sont nombreux. Pour pouvoir les exprimer de façon adaptée à cet outil, il faut les mettre sous la forme d'une fonction « objectif » de plusieurs variables, dont on recherche le maximum (ou le minimum), et surtout la valeur de chacune des variables permettant de l'atteindre, les variables étant soumises à des contraintes (équations, inéquations ou valeurs entières).

Le problème le plus simple d'optimisation appartient au domaine de la programmation linéaire :

• la fonction objectif est une combinaison linéaire de ses variables

• les variables appartiennent à un domaine de valeurs défini de façon linéaire.

C'est sur un exercice TD que nous allons voir le fonctionnement du solveur.