Traitement de données avec tableur appliqué à l'Economie et la Gestion.

Exercice TD

Le but de ce TD est d'écrire différents modèles d'estimation du salaire d'une entreprise par l'ancienneté, la responsabilité et le sexe en utilisant des « régressions linéaires » sur des données artificielles du fichier salaires.txt. Cet exercice correspond à une démarche habituelle de recherche de modèle statistique des données : les relations linéaires sont les plus simples et donc celles qu'on « essaie » en premier, si on ne dispose pas d'autres modèles fournis par des théories des sciences humaines. Suivant cette logique, on commence habituellement par le modèle le plus simple, c'est-à-dire avec une seule variable explicative, et on essaie de l'améliorer. Nous allons réaliser ces différentes étapes à l'aide du tableur. Nous utilisons pour cela principalement la fonction « DROITEREG » du tableur. Bien que nous utilisions les formules matricielles et la loi normale dans ce TP, leur maîtrise n'est pas indispensable car tous les rappels utiles sont faits dans le TP.

Télécharger l'archive (format ZIP) contenant le fichier "salaires.txt"

Modèle 1

Le salaire en fonction de l'ancienneté

Question

Q1 : Recherche du modèle M1 : y=ax+b

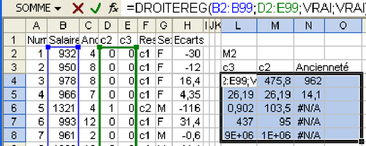
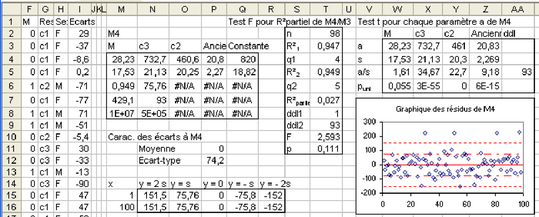
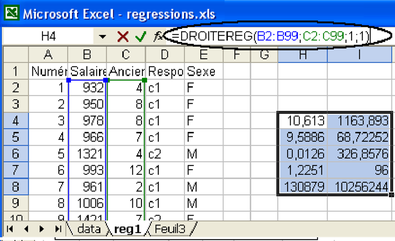
En utilisant la fonction DROITEREG du tableur, trouver les valeurs a et b correspondant à l'équation de régression Salaire = a Ancienneté + b + erreur minimisant les erreurs (voir figure 5.21). Le paramètre b représente le salaire à l'embauche (0 année d'ancienneté) et la valeur de a représente l'augmentation annuelle de salaire, si ce modèle correspond à la réalité, bien sûr.

Figure 5.21 : modèle de régression Salaire=a.Ancienneté + b sur les données du fichier « salaires.txt »

Solution

Question

Q2 : Utilisation du modèle M1 trouvé pour les prédictions et la visualisation

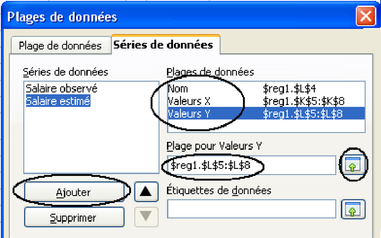
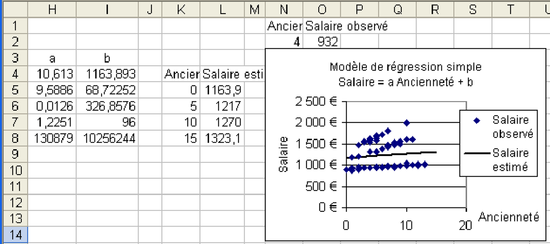
Si on remplace l'ancienneté par un nombre quelconque, on a une estimation du salaire correspondant à cette ancienneté selon le modèle. Écrire dans le tableur quelques valeurs d'ancienneté puis calculer le salaire estimé correspondant en utilisant les valeurs de a et de b obtenues (voir colonnes K et L de la figure 5.22). Faire le graphique permettant de comparer valeurs observées et valeurs estimées comme en figure 5.22.

Figure 5.22 : Utilisation du modèle de régression pour dessiner la droite de régression

Solution

Question

Q3 : Utilisation de l'outil « ajout d'une courbe de régression linéaire » du tableur

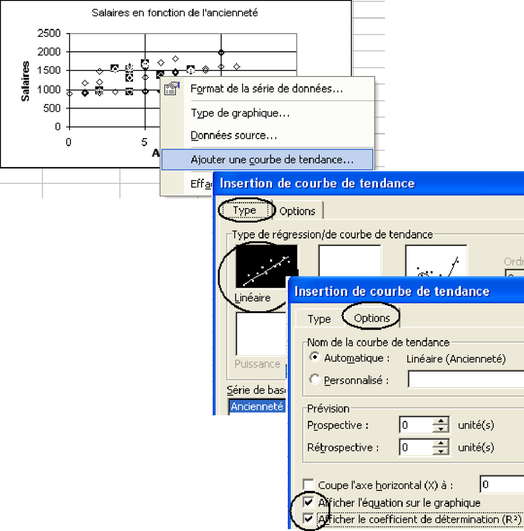
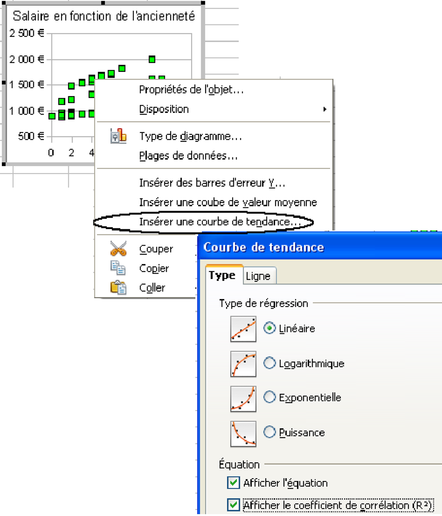
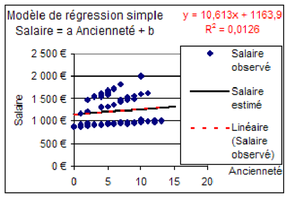
Le tableur permet de dessiner directement les courbes de régression sans faire de calcul. Certains tableurs donnent même l'équation de régression (comme Excel, voir figure 5.23 et OpenOffice3.1). On accède à ces tracés en sélectionnant la série de données, puis en choisissant « Graphique> Ajouter une courbe de tendance » pour Excel et « Insertion>Statistiques » sous OpenOffice. On a alors le choix entre plusieurs courbes de régression. Toutefois cela n'est possible que pour les modèles très simples, comportant une seule variable explicative. Contrôler que la droite que vous avez tracée et la droite de régression dessinée automatiquement par le tableur coïncident, et que l'équation indiquée, ainsi que le coefficient de détermination correspondent bien aux valeurs trouvées avec la fonction DROITEREG.

Figure 5.23 : En rouge la droite de régression linéaire figurant dans les options du graphique avec Excel 2003

Solution

Question

Q4 : Les résidus au modèle M1

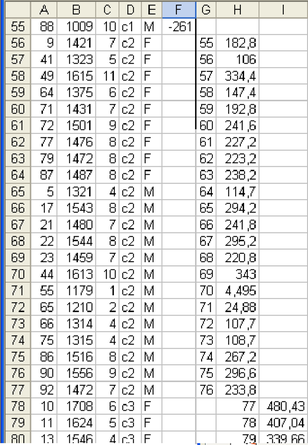
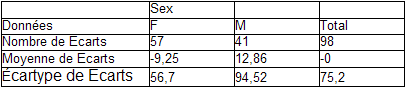
Ajouter une colonne intitulée « écarts » (colonne F de la figure 5.24) contenant pour chaque sujet la différence entre son salaire réel, figurant dans la colonne correspondante, et son salaire estimé d'après l'équation de régression (on utilisera dans la formule, les cellules où figurent a et b, et celles ou figurent x et y). Vérifier qu'on a bien pour moyenne de ces écarts approximativement 0, et pour écart-type, approximativement la valeur figurant dans le tableau à côté de R² (cellules K12 et K13 de la figure 5.24).

Si le modèle est bon, les erreurs suivent une loi normale d'espérance (moyenne) 0, et écart-type s, valeur qui a été rendue par le tableur à côté de R² dans la matrice de résultats. Dans ce cas, on ne doit trouver que 34% des valeurs au maximum à l'extérieur de la bande où y est compris entre –s et s, et au moins 95% des valeurs entre 2s et 2s, le tout étant réparti de façon équilibrée (symétriquement) autour de la droite y=0. Faire un graphique où figurent les points (en utilisant un nuage de points construit sur la seule colonne des écarts) et les droites y=-2s, y=-s, y=0, y=s et y=2s, en insérant des nouvelles données au graphique, ces séries étant situées dans un tableau avec 2 valeurs de x (1 et 100), et pour chacune de ces valeurs, les 5 valeurs de y correspondant aux droites. On doit obtenir le graphique à droite de la figure 5.24.

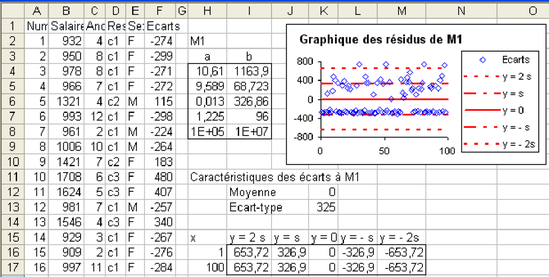
Figure 5.24 : Valeurs des résidus à gauche en colonne F, graphique à droite avec leur répartition en 6 zones devant contenir, en théorie, respectivement 2,5%, 14,5%, 33%, 33%, 14,5%, 2,5% des points.[Zoom...]

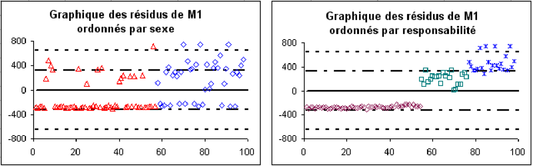
On voit que les conditions de pourcentage paraissent vérifiées (par exemple, on a 4 points dans la première zone à partir du haut, ce qui n'est pas loin des 2,5% attendus), mais pas les conditions de symétrie (au dessus de la droite d'équation y=0, les points s'étalent en hauteur, alors qu'ils sont quasiment alignés sur une droite en dessous de l'axe des x). Pour repérer les individus, trions l'ensemble des colonnes selon le sexe, les femmes se trouvant de la ligne 2 à 58 et des hommes après. On ne voit pas de différences notables entre ces deux parties (figure 5.25 à gauche, F : triangle rouge, M : losange bleu). Faire la même chose en triant selon la responsabilité. On voit (figure 5.25 à gauche, c1 : losange marron, c2 : carré vert, c3 : croix bleue) que pour la responsabilité c1, tous les écarts sont systématiquement négatifs, ce qui signifie que le salaire réel est bien inférieur au salaire estimé, et c'est le contraire pour les 2 autres niveaux de responsabilité. Les conditions de normalité des résidus ne sont plus respectées. On en conclut que le modèle M1 est insuffisant, que la variable « responsabilité » doit intervenir.

Figure 5.25 : Graphique de la figure 5.24 après avoir ordonné par sexe (à gauche), par responsabilité (à droite)[Zoom...]

Solution

Dans la cellule F2, on tape la formule =B2-C2*$H$4-$I$4, et on la recopie vers le bas.

Dans la cellule K12, =MOYENNE(F2:F99) qui doit être 0. On peut toutefois obtenir une valeur très proche de 0 sans lui être égale. En effet les calculs se font en gardant un nombre limité de chiffres après la virgule (la mémoire infinie n'existe pas en informatique), ce qui aboutit à de légers écarts aux valeurs exactes. Ces écarts sont plus importants quand les calculs sont plus lourds, comme pour ceux des coefficients de régression par les moindres carrés qui nécessitent d'inverser une matrice.

Dans la cellule K13, =ECARTYPE(F2:F99), qui donne un résultat proche de celui de la cellule I6, qui est la valeur estimée de l'écart-type des résidus, noté s.

On sélectionne alors la colonne des résidus et on la représente graphiquement par un nuage de points. Les résidus doivent suivre la loi normale N(0,s). Selon cette loi, on connaît les proportions attendues de valeurs dans les intervalles ]-infini, -2s), (-2s,-s), (-s,0), (0,s), (s,2s), (2s, infini[, qui sont respectivement de (ces intervalles sont choisis ainsi par tradition, mais on pourrait en choisir d'autres). En dessinant les 5 droites, cela permet de séparer les points des 6 zones. Pour les tracer, on remplit la zone de H15 à M17 comme indiqué dans la figure 2.24, puis on ajoute ces séries au graphique, en faisant un clic droit sur le graphique sélectionné, puis en choisissant plage de données, et en procédant comme indiqué figure 5.14. Signalons que sous Excel, on peut ajouter en une seule fois la plage correspondant aux 5 droites. On modifie alors le format de chacune pour obtenir la ligne attendue au lieu des 2 points de ses extrémités.

Figure 5.28 : Ajout dans le graphique de la droite de régression linéaire sous OpenOffice 3.1

Figure 5.29 : Les 3 séries décalées de résidus selon la responsabilité, avec ajout des numéros pour c2 et c3

Pour voir la dépendance entre les résidus et le sexe, on sélectionne la plage formée des 6 colonnes et des 99 lignes et on trie selon le sexe. Si on désire différencier les points selon les sexes, comme c'est fait dans le graphique de la figure 5.25, il faut créer 2 séries différentes. Comme la série totale est déjà représentée, on peut la modifier en remplaçant la plage F2 :F99 par F2 :F58, et en insérant une nouvelle série F59 :F99. On peut alors changer le format de chacune. On voit que les résidus ne dépendent apparemment pas du sexe. Inutile donc d'ajouter le sexe dans le modèle M1.

Ce qu'on a fait pour la variable « sexe » est fait de la même façon pour la variable « responsabilité ». On voit cette fois que les résidus dépendent fortement de la responsabilité, qui doit donc être mise dans le modèle.

Sous Excel, il est plus pratique d'insérer directement de nouvelles données, mais il faut les décaler par rapport aux anciennes pour en faire une nouvelle série et non de nouveaux points de la même série, ce qui reviendrait à ce qu'on avait avant. Une fois le graphique fait, on peut les remettre en place (voir figure 5.29).

Modèle 2

La régression linéaire à variables qualitatives

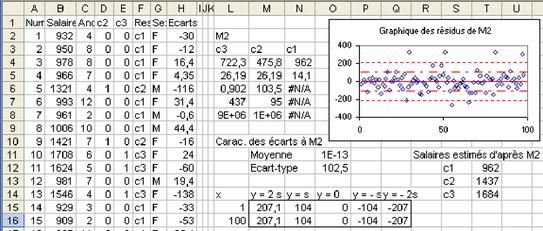
Nous allons utiliser à nouveau la fonction DROITEREG pour estimer le salaire selon la responsabilité. Pour cela il convient de créer des variables numériques exprimant la valeur de la responsabilité. Quand la variable qualitative a p modalités, on crée p-1 nouvelles variables de la façon suivante : une des modalité est la modalité par défaut (par exemple c1), les autres sont des indicatrices des autres modalités (c2 et c3 ici). Il n'y a plus qu'à prendre les colonnes c2 et c3 comme variables X, et écrire le modèle de régression à 3 paramètres exprimant le salaire en fonction de la responsabilité (voir figure 5.30).

Question

Réaliser cette régression comme indiqué dans la figure 5.30, écrire l'équation de régression correspondante, l'utiliser pour calculer le salaire estimé de 3 personnes, une de chaque responsabilité. Représenter graphiquement les résidus. Trouver la valeur de R². Le modèle M2 est-il meilleur que le modèle M1 ? Pourquoi ? Montrer que toutefois l'ancienneté intervient dans les résidus, ce qui invite à créer un modèle M3 prenant en compte la responsabilité et l'ancienneté.

Figure 5.30 : Réalisation du modèle M2 exprimant le salaire en fonction de la responsabilité

Solution

Recodage de la variable responsabilité

Reprendre les données de départ (éviter de prendre celles ordonnées par responsabilité ou par sexe). Insérer 2 colonnes avant la colonne de responsabilité (on peut les créer ailleurs, bien sûr). Ce sont les colonnes D et E de la figure 5.30. En cellule D2, écrire la formule =SI($F2=D$1;1;0), puis la recopier dans la cellule d'à côté et sélectionner ces 2 cellules et tirer vers le bas pour remplir les 2 colonnes. Contrôler que les 1 s'affichent bien à l'endroit voulu.

Écriture du modèle

Ce modèle s'écrit S=a1*c2+ a2*c3 +b + e, et comme il y a 3 paramètres, il faut sélectionner la plage L4 :N8, puis taper la formule =DROITEREG(B2:B99;D2:E99;VRAI;VRAI), et appuyer sur les 3 touches CTRL MAJ Entrée. Taper les lignes d'intitulés du tableau (lignes 2 et 3). L'équation s'écrit Sest.=962 + 475,8 c2 + 733,3 c3. On en déduit que le salaire de base (responsabilité c1 choisie par défaut) est de 962 euros, et qu'il est augmenté de 475 euros environ si on a la responsabilité c2 (soit 962+475) , contre 722 euros s'il a la responsabilité c3 (soit 962+722).

Utilisation du modèle

Ce modèle ne prend en compte que la responsabilité. On a écrit dans la colonne S les 3 valeurs de responsabilité c1, c2 et c3. La formule de calcul du salaire écrite dans T12 est =N$4+M$4*(S12=M$3)+L$4*(S12=L$3). Puis elle est tirée vers le bas, et on retrouve bien les résultats des sommes indiquées dans le paragraphe précédent.

Évaluation de la qualité du modèle

La valeur de R² se trouve dans la cellule L6. Elle est de 0,902, ce qui est très bon. On examine maintenant les résidus. Pour les calculer, on écrit dans H2 la formule =B2-N$4-M$4*D2-L$4*E2, que l'on recopie vers le bas. Les caractéristiques statistiques de ceux-ci sont ensuite calculées. La moyenne fait approximativement 0, comme attendu, et l'écart-type est proche de sa valeur théorique écrite dans la cellule M6. On représente alors le nuage des résidus avec les 6 zones délimitées par les 5 droites. Il a l'air de suivre à peu près la loi normale (en cas de difficulté pour réaliser cette partie, voir les explications détaillées correspondantes du modèle M1).

Indépendance des résidus et des autres variables

Ce modèle est bon, mais on peut peut-être l'améliorer en faisant entrer les autres variables dans le modèle. Pour cela on regarde si les résidus sont liées à d'autres variables, par exemple l'ancienneté. On représente graphiquement les résidus de M2 en fonction de l'ancienneté et le nuage de points montant indique clairement qu'il y a une liaison positive entre les 2 (voir figure 5.31). On ajoute la droite de régression (une fois le graphique sélectionné, par un clic droit, on peut lui ajouter une tendance, qu'on choisit linéaire), son équation et le R² correspondant, ce qui confirme clairement la liaison, et invite à faire un modèle de régression avec les deux variables explicatives, ancienneté et responsabilité.

Figure 5.31 : Les résidus de M2 sont une fonction croissante de l'ancienneté

Modèle M3

La régression linéaire multiple à deux variables mixtes

Question

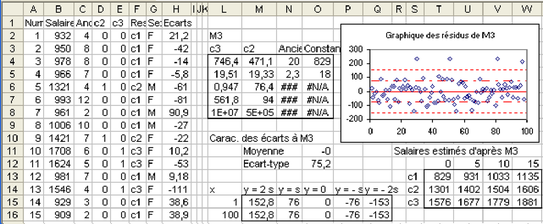
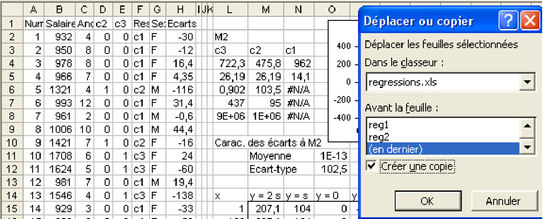
Q1. Faire une copie de la feuille de calcul (voir Figure 5.32), puis corriger afin de prendre dans les variables explicatives à la fois l'ancienneté et la responsabilité. Écrire l'équation du modèle M3 trouvé puis faire un tableau donnant les estimations de salaires pour 12 personnes, dont l'ancienneté prend les valeurs 0, 5, 10, 15 et les 3 responsabilités c1, c2 et c3.

Figure 5.32 : copie de la feuille de calcul contenant le modèle M2 pour la corriger en un modèle M3 sous Excel

Solution

Question

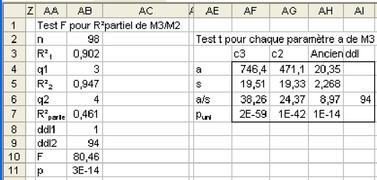
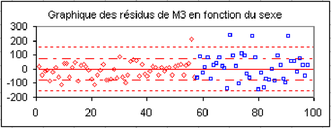
Q2. Le modèle M3 est-il bien meilleur que le modèle M2 ? Pour tester la significativité de l'augmentation de R², c'est-à-dire le fait que cette augmentation n'est pas due au hasard, plusieurs méthodes existent dans le cas de modèles emboîtés, la plus ancienne étant de calculer la statistique R²partiel/(1-R²partiel)/(q2-q1)*(n-q2) avec R²partiel=(R²2-R²1)/(1-R²1), où R1 et R2 sont les coefficients de détermination respectifs de M2 et M3, qui doit suivre la loi de Fisher Snedecor (appelée loi.F dans les fonctions du tableur), à (q2-q1) et (n-q2) degrés de liberté, q1 et q2 étant le nombre de paramètres respectifs de M2 et M3, soit ici 3 et 4. Quelle est votre conclusion ? Examiner les résidus, seuls, puis groupés par sexe. A votre avis la variable sexe doit-elle être mise dans le modèle ?

Solution

le R² est passé de 0,906 à 0,947, ce qui indique une amélioration, mais elle n'a pas nécessairement de sens. En effet chaque fois qu'on ajoute une variable, la valeur de R² augmente généralement, au point que si on met autant ou plus de variables que d'individus, on peut obtenir un R² de 1. Il faut contrôler que l'augmentation de R² a un sens (du point de vue statistique). Nous avons proposé d'utiliser pour cela la statistique F=R²partiel/(1-R²partiel)/(q2-q1)*(n-q2) avec R²partiel=(R²2-R²1)/(1-R²1), on peut voir les résultats du calcul dans la cellule AB10, et la probabilité p d'avoir un R²partiel aussi grand par hasard est inférieure à 0,01, ce qui nous permet de conclure que le R²partiel est très significatif, et que le passage du modèle M2 au modèle M3 est justifié statistiquement.

pour trouver exactement les mêmes valeurs que dans la figure 5.35, il faut veiller à écrire dans les formules les adresses des nombres si ceux-ci ne sont pas entiers, et non les valeurs qu'on voit à l'affichage, car ce sont leurs valeurs approchées (par exemple dans la cellule AB3 la formule est =reg2!L6). La valeur de p se trouve par la formule LOI.F(AB10;AB8;AB9) écrite dans AB11.

On peut aussi tester la significativité de chaque paramètre du modèle (c.à.d. qu'ils diffèrent significativement de 0). Le test peut être bilatéral (on ne sait pas s'ils risquent d'avoir un effet positif ou négatif sur le salaire), ou unilatéral. Ici on suppose que l'ancienneté, la responsabilité élevée ont un effet positif sur le salaire, c'est un test unilatéral. Pour calculer la statistique t = a/s, on utilise les deux premières lignes du modèle de régression. On sait que si t dépasse largement 2, et que le ddl est élevé, comme ici, la probabilité p d'avoir une valeur si grande par hasard sera très faible. Elle est calculée dans la ligne 7. Dans la cellule AF7 on a la formule =LOI.STUDENT(AF6;$AI6;1) qu'on recopie vers la droite. On obtient que toutes les valeurs de p sont inférieures à 0,01 et donc que les 3 paramètres sont très significatifs. Il est à noter que le passage de M2 à M3 porte sur une seule variable, la variable ancienneté, et comme elle est unique, on a la relation entre la valeur tancienneté et FM3/M2 : t²=F. Et quand on prend un test bilatéral, ce qui n'est pas le cas ici, on trouve la même probabilité avec t ou avec F. Avec un test unilatéral, on trouve une probabilité associée à F double de celle associée à t.

Figure 5.35 : Réalisation du test de significativité du modèle M3/M2 à gauche et de tous les coefficients de l'équation de régression de M3 à droite. Tout est très significatif, les valeurs de p étant <0,01

Le calcul des résidus doit être aussi mis à jour. La formule dans H2 est =B2-O$4-M$4*D2-L$4*E2-C2*N$4 et on la recopie vers le bas. A ce moment-là, dans les caractéristiques des résidus, la moyenne passe à 0 et l'écart-type devient peu différent du contenu de la cellule. Les équations des 5 droites sont mises à jour et le graphique des résidus également. Si on fait le graphique des résidus en fonction du sexe, on voit que les résidus des femmes (losanges rouges) sont plus groupés autour de l'axe que ceux des hommes (carrés bleus)., ce qui montre une différence de variance.

Figure 5.36: Les résidus de M3 diffèrent selon le sexe

On vérifie cela par un tableau croisé dynamique donnant les statistiques des écarts. On constate alors que non seulement les variances (ecart-type²) diffèrent mais également les moyennes. Ce qui invite à prendre en compte le sexe dans le modèle.

Tableau 1

Modèle 4

La régression linéaire multiple avec 2 variables qualitatives et une quantitative

Question

Q1 : Ajouter la variable sexe dans le modèle. Pour cela insérer une colonne à coté des colonnes des autres variables, en prenant par exemple la variable F par défaut (1 si sexe= ‘M', 0 si sexe='F'). Puis écrire le modèle. Et tester son apport par rapport à M3.

Solution

Modèle 5

La régression linéaire multiple avec interaction entre 2 variables

On repart de M3, et on essaie de l'améliorer par la prise en compte d'autres effets. On désire prendre en compte une augmentation annuelle de salaire différente selon les responsabilités. Cela s'appelle une interaction entre la variable responsabilité et la variable ancienneté. Pour cela on ajoute la variable produit des deux, donc deux colonnes supplémentaires, Ac2 et Ac3, qu'on obtient par produits respectifs des colonnes A et c2, A et c3), ce qui donne S = a1 A + a2 c2 + a3 c3 + a4 A c2 + a5 A c3 + b + e (on dit encore que le modèle est linéaire car il est une combinaison linéaire des paramètres à estimer a1, a2, ..., a5, b, mais certains auteurs ne disent plus régression linéaire dans ce cas, comme dans le cas où des variables sont élevées à une puissance quelconque).

Question

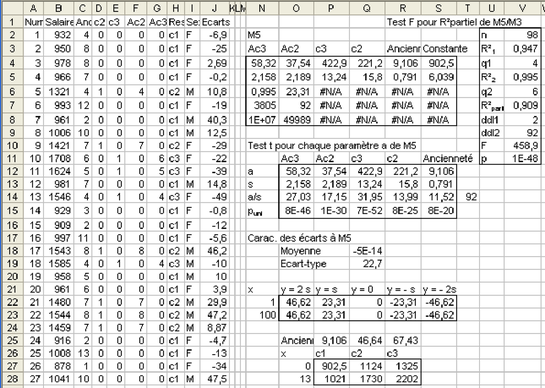
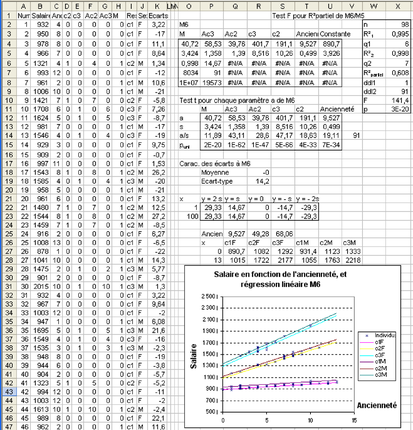
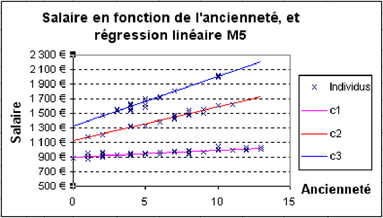
Q1. Ajouter ces deux variables dans des colonnes et estimer le modèle, et tester son apport par rapport à M3. Donner l'équation générale du modèle, ainsi que les équations par responsabilité. Puis représenter graphiquement le nuage de points ainsi que les 3 droites de régression du salaire sur l'ancienneté pour chaque responsabilité (voir figure 5.38).

Figure 5.38 : Nuage de points et modèle de régression avec interaction sous la forme de 3 droites

Solution

Question

Q2. Tester le modèle M5 par rapport au modèle M4. Ainsi que les paramètres du modèle. Représenter les résidus en fonction du sexe. On voit que cette fois la différence est bien visible entre les résidus des 2 sexes. Il faut donc essayer à nouveau de faire entrer le sexe dans le modèle. Écrire le modèle M6 et le tester.

Solution

Exercices TD pour la leçon 5 (page suivante)La régression linéaire (page Précédente)

Accueil Pôle de Recherche et d'Enseignement Supérieur de l'Université de Lorraine