La régression linéaire
Les modèles de régression permettent d'ajuster une variable quantitative y, appelée variable à expliquer (ou variable dépendante), à une fonction f de variables quantitatives ou même qualitatives, appelées variables explicatives (ou variables indépendantes, ou régresseurs).
Par exemple, on donne parfois comme relation entre la taille x d'un individu adulte et son poids idéal y l'équation y = (x-100) - (x-150)/4 soit y = 0,75x - 62,5. Parmi ces modèles, f(x)=ax+b est le modèle le plus simple de régression linéaire, qui permet d'ajuster le nuage de points (x, y), où x et y sont deux variables quantitatives, à la droite d'équation yest. =ax+b, également appelée droite de régression de y sur x. Dans cette équation, yest. est la valeur de y estimée selon le modèle, et non la valeur de y observée dans les données, leur différence yobs.-yest. étant ε, appelée résidu (ou erreur, ou écart au modèle). Dans l'exemple précédent, yest. est le poids idéal d'un individu de taille x, qui diffère généralement de son poids réel yobs.. Les paramètres a et b du modèle, respectivement appelés pente de la droite et ordonnée à l'origine sont calculés à partir de toutes les valeurs de x et de y avec la méthode des moindres carrés ordinaires, que nous ne détaillerons pas ici, le tableur se chargeant de tous les calculs. La qualité explicative globale de ce modèle est mesurée en partie par la corrélation linéaire (coefficient de corrélation linéaire de Bravais-Pearson) existant entre la valeur estimée et la valeur réelle, ou plutôt par son carré R², appelé coefficient de détermination, qui exprime le pourcentage de variation de y expliqué par le modèle.
Si le modèle de régression linéaire simple parait insuffisant pour expliquer y, on peut ajouter d'autres variables explicatives. Avec p variables, l'une à expliquer et les autres explicatives, le nuage de points dans l'espace de dimension p peut être ajusté à un hyperplan de dimension p-1 d'équation yest.=a1x1+a2x2+... apxp+b, le modèle correspondant étant appelé modèle de régression linaire multiple. Quand p=3, on dit qu'on a un plan de régression. Plus le nombre de variables augmente, plus la valeur de R² augmente également. Malgré tout, le meilleur modèle n'est pas généralement celui comportant le plus grand nombre de variables explicatives.
La régression linéaire avec le tableur
Si on dispose d'un tableau de données de p variables pour n individus, la régression de l'une des variables sur les p-1 autres s'obtient par la fonction DROITEREG(y ; x ; constante; statistiques), où y est la colonne de n valeurs de la variable à expliquer, x sont les p-1 colonnes de n valeurs des variables explicatives, constante est à VRAI si on accepte une valeur de b non nulle, et statistiques est à VRAI si on désire avoir des informations statistiques autres que les valeurs de paramètres. Le résultat de cette fonction est le tableau ayant les p colonnes et 5 lignes suivantes quand constante; statistiques sont à VRAI (p=4 dans celui-ci):

Dans la première ligne on a les paramètres du modèle, dans la ligne suivante, leurs écarts-types, et R² en dessous. Les autres valeurs sont utilisées pour construire des tests statistiques. Les cases grisées ne sont pas remplies de valeurs, mais de codes d'erreur. Pour obtenir le tableau de résultats, comme on désire plusieurs valeurs, on procède comme pour le calcul matriciel du tableur : on sélectionne la zone de p colonnes et 5 lignes, on tape =droitereg( , on sélectionne alors la colonne des y, puis les colonnes des x, et vrai et vrai, ces 4 arguments étant séparés par des point-virgule, et après avoir fermé la parenthèse, on valide en enfonçant simultanément les 3 touches adéquates, CTR, MAJ, Entrée..
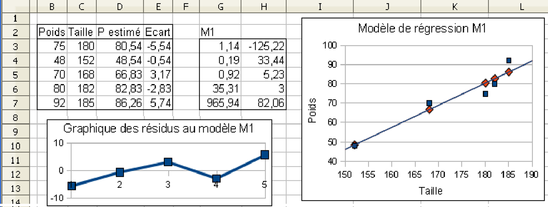
Dans la figure 5.19, on a 5 colonnes de valeurs pour 5 individus de B4 à F8. Le premier modèle de régression, M1, est écrit dans les cellules de H4 à I8. Sa formule est =DROITEREG(B4:B8;C4:C8;1;1). Avec le résultat figurant dans les cellules H4 et I4, on peut écrire le poids en fonction de la taille par la formule :
Poids est. = 1,14*Taille-125,22
La qualité de ce modèle est élevée car R² = 0,92 (cellule H6), valeur proche de 1.
Modèle M2 : Poidsest. = 0,83*Taille - 0,3*Age - 57,65, R²=0,94, =DROITEREG(B4:B8;C4:D8;1;1).
Modèle M3 : Poidsest.=0,86*Taille-0,18*Age-0,003*Salaire-64,44, R²=0,95, =DROITEREG(B4:B8;C4:E8;1;1).

On peut remarquer que la valeur de R² est très forte pour M1, et qu'elle augmente très légèrement quand on passe de M1 à M2 puis M3. Ces trois modèles sont dits emboîtés car les ensembles de variables qu'ils utilisent sont inclus les uns dans les autres, et on peut calculer la significativité, au sens statistique du terme, de ces augmentations (les lecteurs intéressés peuvent consulter les ouvrages de G. Baillargeon sur la régression linéaire, par exemple celui intitulé « La régression linéaire » aux éditions des Trois Sources, Québec, 2000). Seul le premier modèle a vraiment un sens.
Dans la figure 5.20, on a analysé les apports du modèle M1. La colonne D a été remplie avec les valeurs estimées de P selon ce modèle (en D3, on a =C3*G$3+H$3), en colonne F les écarts P-Pest. ont été calculés (en C3, on a =B3-D3). À droite de la figure, on a représenté graphiquement trois séries :
-
la série des points observés, indiqués par des carrés bleus, avec la taille en abscisse et le poids observé en ordonnée
-
la série des points estimés, indiqués par des losanges rouges, avec la taille en abscisse et le poids estimé d'après le modèle M1 en ordonnée
-
la droite de régression dessinée automatiquement par le tableur (sélection de la série de valeurs observées puis ensuite insertion> tendance linéaire)
On peut contrôler que la droite de régression passe bien par tous les points estimés, et que le nuage de points bleus est très allongé, ce qui est cohérent avec un R² proche de 1.
Les conditions de validité d'un modèle de régression linéaire
La connaissance de R² est importante pour apprécier la qualité de ces modèles mais elle ne suffit pas. En effet ces modèles de régression linéaire ainsi estimés d'après les données ne sont vraiment utiles que s'ils permettent de faire des prédictions réalistes, par exemple de « prédire » réellement le poids d'un individu sachant sa taille. Pour cela il faut que les hypothèses statistiques sur lesquelles s'appuient les modèles de régression linéaire soient respectées (pour plus de détails, se référer à l'ouvrage « Comment interpréter les résultats d'une régression linéaire? » de R. Tomassone, édité par l'ITCF, Paris, 1997). Voici les trois plus importantes, les deux premières sont préalables à la construction du modèle, la denrière doit être vérifiée une fois celui-ci sonstruit, avant son utilisation.
-
La plus importante pour un modèle statistique, difficile à contrôler après coup, impose que les données aient été recueillies et soient utilisées selon la théorie de l'échantillonnage. Dans notre cas très simple de régression linéaire, il faut que les personnes interrogées soient un échantillon représentatif de la population sur laquelle on compte appliquer le modèle. Rappelons que faire des statistiques sur des données dont on ignore la provenance ne peut conduire qu'à des conclusions sans aucune valeur scientifique.
-
Même si les données ont été collectées en respectant les règles de la théorie de l'échantillonnage, il faut vérifier qu'il n'y a pas de données aberrantes (un homme de 300 cm, de 20 kg, etc.) dues à des erreurs humaines de saisie. Par exemple, pour le modèle M1 de la figure 5.20, un graphique permet de contrôler qu'il n'y a pas de données aberrantes, c'est-à-dire qui « dépassent » du nuage de points de dimension 2 (points bleus dans le graphique à droite de la figure 5.20). Quand la dimension du nuage de points augmente, il faut examiner la distribution des variables une à une.
-
Les résidus doivent être i.i.d. (Indépendamment Identiquement Distribués). On peut essayer de vérifier cela par un certain nombre de graphiques. Par exemple dans la figure 5.20, en bas à gauche, on a représenté la succession des 5 résidus. On peut voir qu'il y en a à peu près autant de positifs que de négatifs, mais avec si peu de valeurs on ne peut pas vraiment dire que les valeurs proches de 0 sont plus nombreuses que celles éloignées de 0, comme l'impose la loi normale. Cette loi est souvent postulée pour permettre d'obtenir des intervalles de confiance des valeurs prédites.
