Cours (suite)
3 Graphe sagittal
31 Pert potentiel-étapes
Nous allons établir le graphe sagittal pour le Pert potentiel étapes.
Dans cette méthode chaque tâche est représentée par un vecteur orienté dans le sens du déroulement du temps mais de longueur arbitraire.
Chaque vecteur part d'une étape pour arriver à une autre c'est une liaison entre deux tâches.
La succession de vecteurs constitue un chemin.
Remarque la numérotation des tâches est arbitraire.
Prenons l'exemple précédent pour lequel la répartition des tâches en niveaux est :
et la liste des tâches et de leurs antériorités :
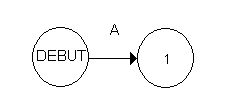
Nous allons débuter le graphe avec les tâches de premier niveau dans notre cas il s'agit de la tâche A :
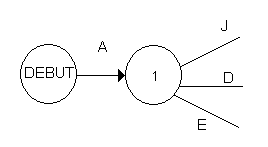
Ensuite les tâches D,E, et J les tâches de deuxième niveau, elles ont toutes les trois la tâche A pour antécédent[1]. Elles peuvent donc débuter en même temps cela se représente sur le graphe par des vecteurs en parallèle.
Puis nous allons placer les tâches de troisième niveau B,C et F sachant que B et C ont pour antécédent E et que F a pour antécédent D et E.
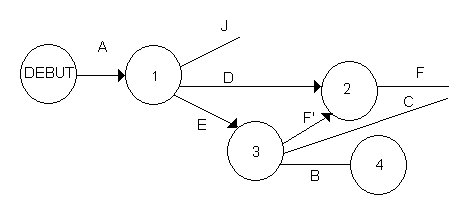
Remarque :
pour indiquer que F a pour antécédent D et E nous avons été obligés d'introduire une tâche fictive F' cette tâche est de durée nulle. Elle indique simplement que pour démarrer F il faut avoir fini D mais aussi E.






