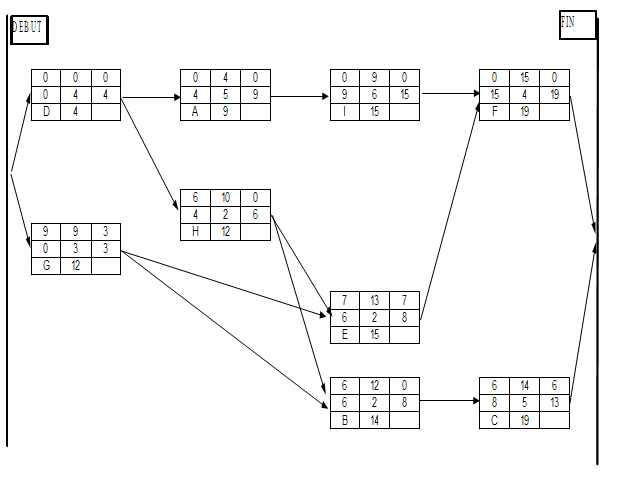
L'entreprise Ordoméca met à l'étude le lancement d'une nouvelle gamme de produits.
Ce lancement nécessite la réalisation de tâches[1] repérées par les lettres A à I et dont les caractéristiques sont les suivantes :
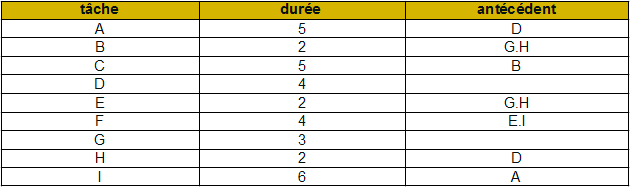
si vous avez déjà résolu les premières questions passez directement à la question 3.
[Anglais : Task] [Espagnol : Tarea]
Action d'une ampleur limitée, la tâche appartient à un métier donné et correspond généralement à une division de l'activité; ses caractéristiques, en particulier quantitatives (coût et durée), peuvent faire l'objet de séries statistiques qui donnent lieu à un calcul de probabilités.
C'est l'élément le plus fin d'un planning de réalisation.
[Anglais : Precedence] [Espagnol : Método francés]
À partir de la théorie des Graphes qui comprend deux types d'éléments, les sommets et les arcs, deux types de réseaux sont utilisés en planification : ceux dont les contraintes potentielles (contraintes de succession et contrainte de localisation temporelle) s'expriment par l'intermédiaire des sommets (étapes dans un réseau PERT ) et ceux dont les contraintes potentielles s'expriment par les arcs, de tâche à tâche.
Les méthodes PERT et CPM ont une représentation «potentiel-étapes » -, la méthode des potentiels (méthode MPM) et la méthode des antécédents (méthode PDM) sont représentées en « potentiel-tâches ».
[Anglais : Step] [Espagnol : Etapa, Nudo]
Ne pas confondre étape et événement . C'est le point de liaison entre des activités amont et des activités aval, où le début de chaque activité aval est conditionné par l'achèvement de toutes les activités amont.
Le nombre de liaisons que contient une étape est égal au produit du nombre de ses activités amont par le nombre de ses activités aval. Mathématiquement, c'est l'application d'un ensemble de NI événements amont dans un ensemble de N2 événements aval; le nombre de liaisons est donné par le produit cartésien N = NI x N2 Relations d'ordre. Exemple - 2 x 3 = 6 liaisons. En méthode PERT , l'étape est représentée par un cercle qui reçoit NI liaisons amont et émet N2 liaisons aval, soit au total NI + N2 liaisons.
Dans les méthodes par liaisons individualisées, l'étape n'est pas exprimée. Elle est traduite par les NI x N2 liaisons précédentes.
