Les données sont discrètes
Représentation des données brutes
On dispose dans le fichier « data_discretes.txt » de données X pouvant prendre des valeurs entières à partir de 0, recueillies auprès d'un échantillon de N personnes. Les copier dans une feuille Excel, les trier par valeurs croissantes, et calculer leurs caractéristiques statistiques N, moyenne, écart-type (Fig. 6.1 : B11 à B13). Puis trouver les effectifs correspondant à chaque valeur (plage C14 :D26).
L'ajustement de trois lois théoriques
Les lois de probabilités utilisées pour ajuster ces données sont :
-
la loi uniforme
-
la loi binomiale
-
la loi de Poisson
La loi uniforme a pour seul paramètre le nombre de valeurs, que nous avons choisi ici égal à 11. Le somme des effectifs pour chaque valeur de X1 est la même et l'effectif total est N, ce qui fait que chaque effectif est de nombre_classes/N.
La loi binomiale représente le nombre de succès obtenus en répétant n fois de façons indépendantes une expérience ayant une probabilité p de succès. Nous prenons pour n un entier entre 10 et 20, et pour p une valeur entre 0 et 1 variant avec un pas de 0,01.
La loi de Poisson représente le nombre de survenues d'un événement rare pendant une période donnée, sachant qu'une nouvelle occurrence de cet événement peut arriver à tout moment de la période, indépendamment de l'arrivée de l'occurrence précédente, avec en moyenne occurrences pendant la période.
Comme dans la partie précédente, on utilise des barres de défilement pour ajuster les paramètres des lois. Pour pouvoir comparer les lois théoriques à la distribution empirique des données, on regroupe les valeurs en classes, puis on compare les effectifs selon la distance du Chi2. Le regroupement est fait dans les cellules C28 à G31 et donne la série X2, représentée par un histogramme dans le graphique du haut de la figure 6.10, alors que la série X1 est représentée dans celle du bas par une courbe très accidentée, donc peu exploitable pour l'ajustement. Les écarts correspondant à X2 sont calculés dans la plage D33 :G37. L'ajustement se fait en observant les valeurs de la ligne 37, somme des 3 valeurs au dessus, la cellule E34 contenant la formule « =(E29-D29)²/E29 », qui est recopiée vers la plage E34 :G36 une fois les $ ajoutés si nécessaire.

Réaliser le travail correspondant à la figure 6.11. La loi de Poisson parait la plus ajustée aux données. Aurait-on pu obtenir mieux par la méthode des moments ? Et que donne le solveur ?
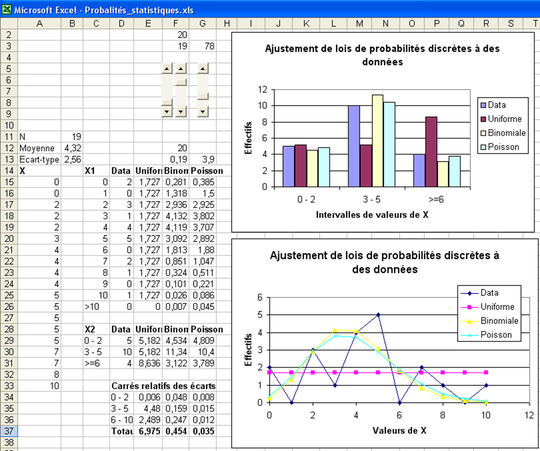
Correction
Dans F12 =F2
Dans F13 =F3*0,01
Dans E15 = =$B$11/NB($C$15:$C$25)
Dans F15 =LOI.BINOMIALE(C15;F$12;F$13;0)*$B$11
Dans G15 =LOI.POISSON(C15;G$13;0)*$B$11
Dans D29 =SOMME(D15:D17)
Dans E34 =(E29-$D29)*(E29-$D29)/E29
Dans E37 =SOMME(E34:E36)
