Les données sont continues
Représentation des données brutes
On dispose dans le fichier « data_continues.txt » de données X pouvant prendre toute valeur comprise entre 0 et 5 recueillies auprès d'un échantillon de N personnes. Les copier dans une feuille Excel, les trier par valeurs croissantes, et calculer leurs caractéristiques statistiques N, moyenne, écart-type (Fig. 6.1 : B11 à B13) ainsi que leurs fréquences cumulées (colonne B).
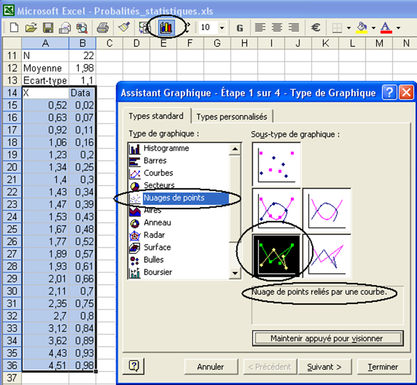
Aide :
Les fréquences cumulées sont habituellement les valeurs k/N avec k= 0, 1,..., N-1, N. Pour faciliter l'ajustement aux lois de probabilités continues, on a choisi k=0,5 ; 1,5 ; N-0,5.
Après sélection des deux colonnes de données, on appelle l'assistant graphique (en cliquant sur l'icône correspondant, ou en allant dans les menus déroulants Insertion>graphique sous Excel, ou insertion>diagramme sous OpenOffice).
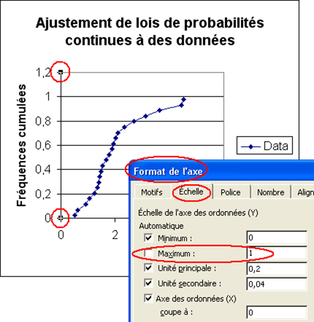
Dans l'étape 1 de l'assistant graphique, on choisit la représentation graphique adaptée (« nuage de points sous Excel », « diagramme XY » sous OpenOffice), et on remplit pour chaque étape les champs demandés, puis on sélectionne le graphique afin qu'il ressemble à celui de la figure 6.2.
Si vous ne savez pas comment remplir les champs ou choisir les options parmi celles proposées dans les diverses fenêtres de l'aide, vous pouvez valider sans remplir aucun champ. Il suffit alors de sélectionner le graphique obtenu (par un simple clic sous Excel, et un double clic sous OpenOffice) et de corriger un à un les divers éléments en les sélectionnant par un clic gauche puis en choisissant leur format par un clic droit. On peut voir dans la figure 6.2 la modification du format de l'axe des y.
Les objets du graphique sont atteignables par un clic gauche une fois le graphique sélectionné, à condition qu'ils existent dans le graphique. Si ce n'est pas le cas, par exemple pour le titre, les intitulés des axes, la légende, il faut d'abord les ajouter. Pour cela dérouler le menu « insertion » une fois le graphique sélectionné, et remplir alors les champs demandés.
Sous Excel, on peut faire défiler les divers objets du graphique (zone de graphique, zone de traçage, titre du graphique, légende, axes, séries de points, grille secondaire) par les touches de déplacement vers le haut et vers le bas du clavier, puis les divers éléments d'un objet par les touches de déplacement gauche et droite, par exemple les points successifs d'une série si on veut changer la couleur de l'un d'eux, les divers éléments de la légende, chacun des axes, etc.
Ajustement de la loi normale aux données
On choisit une espérance et un écart-type quelconques (par exemple dans C12 une espérance de 2,5 et dans C13 un écart-type de 10, voir Fig. 6.3), et on crée dans la colonne C les données de la loi de répartition normale N(2,5 ;10) en écrivant dans C15 la formule « =LOI.NORMALE(A15;C12;C13;1) », puis en la recopiant vers le bas après avoir ajouté les $ aux endroits appropriés. Puis on ajoute la courbe correspondante à celle des données brutes.
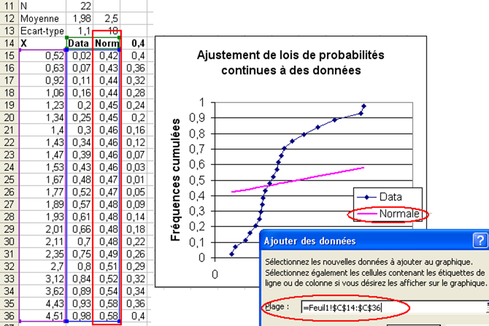
On peut voir sur la figure 6.3 que la courbe de la loi normale diffère beaucoup de la courbe des données. Cela est dû au mauvais choix des paramètres de la loi normale (espérance, écart-type). Nous allons essayer d'améliorer l'ajustement en faisant un choix plus judicieux.
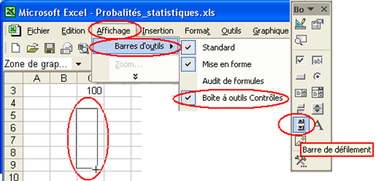
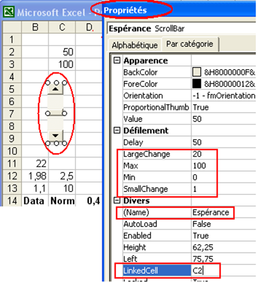
Plutôt que de saisir successivement de nombreuses valeurs, nous créons une barre de défilement (voir Fig. 6.4) dont le rôle est de remplir la cellule C2 d'un nombre entier compris entre 0 et 100, en allant de 1 en 1 (petit changement : SmallChange) ou de 20 en 20 (grand changement : LargeChange). Un clic droit sur la barre de défilement créée permet d'atteindre les propriétés de celle-ci et de saisir ses paramètres (voir en rouge sur la figure 6.5).
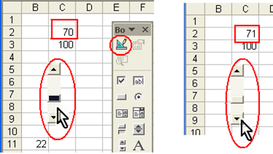
Après un clic sur l'icône du « mode création » (en haut à gauche de la « boite à outils contrôles ») pour le désactiver, on utilise la barre de défilement pour modifier le contenu de la cellule C2, comme indiqué figure 6.6.
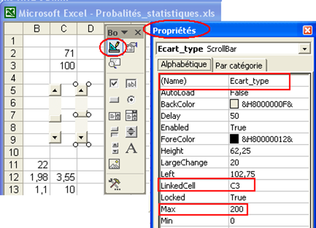
On crée ensuite la barre de défilement pour la cellule C3. On peut procéder comme précédemment, ou activer le « mode création », faire un copier-coller de la barre de défilement précédente, et modifier ses propriétés (voir Figure 6.7).
Les deux cellules C2 et C3 contenant des nombres entiers qui peuvent varier par pas de 1, on peut faire varier par pas de 0,05 l'espérance en tapant dans la cellule C12 la formule « =C2*0,05 », et par pas de 0,1 l'écart-type en tapant dans la cellule C13 la formule « =C3*0,1 ».
Il ne reste plus qu'à déplacer les barres de défilement pour obtenir la courbe la plus ajustée aux données. Pour rendre la recherche plus facile, on peut s'aider d'un indicateur d'écart entre les deux courbes, par exemple est la plus grande distance verticale. Pour cela on a écrit dans la colonne D (voir Fig. 6.8) pour chaque point les écarts verticaux entre les deux courbes, et en D14 le maximum de ces écarts, qui est à minimiser.

On peut voir dans la figure 6.8 le résultat sur le graphique du choix de bons paramètres pour cette loi, choix facilité par les barres de défilement. A ce choix correspond un écart vertical de 0,18. Par la méthode des moments, pouvez-vous obtenir mieux ? Et par tâtonnement ? En utilisant le solveur ?
Ajustement de deux autres lois continues aux données
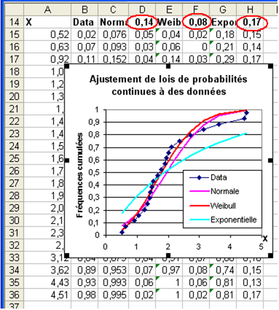
On propose d'ajuster de la même façon la loi de Weibull et la loi exponentielle aux données. On peut voir le résultat dans la figure 6.9 ci-dessous. La loi la plus ajustée aux données semble être la loi de Weibull. Réaliser les calculs et le graphique.
Correction
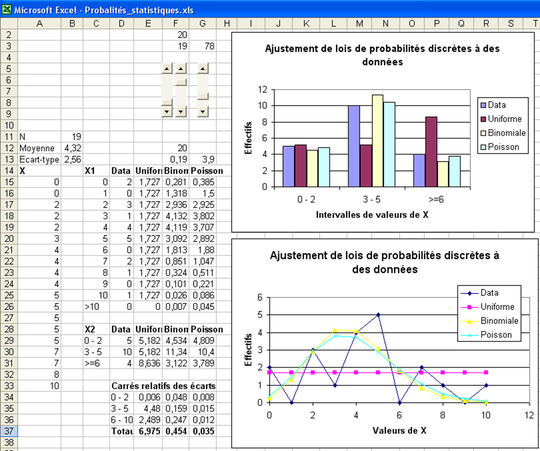
Pour la loi de répartition des données
Cellules saisies directement : colonne A, B14, C14, lignes 2 et 3.
B11 =NB(A15:A36)
B12 =MOYENNE(A15:A36)
B13 =ECARTYPE(A15:A36)
B15 =0,5/B11
B16 =B15+1/B$11
copier-coller de B16 jusqu'à B36
Réaliser le graphique avec les données des colonnes A et B (sélectionner la plage de A14 à B36).
Pour la loi normale :
en C2 et C3 des valeurs entières quelconques, par exemple 50 et 100
C12 =C2*0,05
C13 =C3*0,1
C15 =LOI.NORMALE($A15;C$12;C$13;1)
copier-coller de C15 jusqu'à C36
D14 =MAX(D15:D36)
D15 =ABS(B15-C15)
copier-coller de D15 jusqu'à D36
Ajouter au graphique la fonction de répartition de la loi normale
lignes 2 et 3 remplies avec "Barre de défilement de nombres entiers utilisés pour faire varier les paramètres (ces nombres multipliés par 0,1 ou 0,01, ou ...) des lois situés dans les lignes 12 et 13.
Faire varier les valeurs de l'espérance et de l'écart-type pour trouver une courbe de loi normale qui ait un écart minimum (contenu de la cellule D14) avec celle des données.
Etirer la plage C2:D36 pour qu'elle aille de C2 à H36
Remplacer l'intitulé "Normale" par Weibull puis Exponentielle
et la formule de la loi normale par les lois correspondantes :
E15 =LOI.WEIBULL($A15;E$12;E$13;1)
G15 =LOI.EXPONENTIELLE($A15;G$13;1)
et les étirer vers le bas.
Puis supprimer le contenu des cellules G2 et G12.
Insérer ces nouvelles lois de répartition dans le graphique.
