< retour au sommaire

Exposé :

La notion de coûts partiels recouvre l’ensemble des coûts calculés dans une optique de décision à court/moyen terme. La méthode du coût variable constitue une des techniques principales fondées sur la prise en charge partielle des coûts d’un produit. Elle repose sur la classification qui a été faite dans la leçon 2, à propos des typologies de coûts. Ceux-ci sont donc composés de l’ensemble des charges variables directes et indirectes liées au produit. Néanmoins, il faut garder à l’esprit qu’ils ne constituent qu’une représentation de la réalité. Il est donc nécessaire de préciser leur portée et leurs limites, avant d’exposer le modèle du seuil de rentabilité.

1.  Les coûts variables : objectifs et hypothèses

Comme pour tout modèle, il est nécessaire d’en préciser dans une première étape, les objectifs, puis nous verrons dans une seconde étape, sur quelles hypothèses il repose.

1.1. Les objectifs

Le direct costing ou méthode des coûts variables est intrinsèquement lié au seuil de rentabilité. L’estimation par les coûts variables est une technique à laquelle on a souvent recours, parce que cette dernière répond à plusieurs objectifs :

1°)  en tout premier lieu, elle permet de juger la performance des responsables ;

2°)  de manière corollaire, elle permet naturellement d’apprécier la profitabilité globale des produits fabriqués ou vendus, puisque à partir du moment où la marge globale sur coût variable est supérieure aux frais fixes, cela signifie que l’entreprise commence à réaliser des bénéfices ;

3°)  elle autorise un diagnostic de la rentabilité des produits, à partir de la marge sur coûts variables qu’ils dégagent. On peut choisir d’en développer certains, pour ceux qui présentent des taux de marge importants ou d’en abandonner d’autres. Il faut cependant être prudent avant de porter un diagnostic définitif sur la bonne rentabilité présumée d’un produit à partir du seul critère de la marge, en raison des coûts fixes spécifiques que ce dernier peut être amené à supporter ;

4°)  en cas de sous-traitance, elle peut permettre d’apprécier la rentabilité de l’opération, puisque cette dernière permet de « variabiliser » les charges fixes que constituent les salaires ;

5°)  enfin, elle permet de choisir également s’il faut ou non produire plus de produits dans certains cas, car elle constitue le prix minimum à appliquer pour des séries marginales.

1.2. La notion de coût variable ou proportionnel et ses limites

Les coûts variables comprennent l’ensemble des charges variables directes et indirectes. Le modèle repose sur une hypothèse fondamentale, à savoir que les coûts variables sont exactement proportionnels aux quantités fabriquées. Ces derniers sont d’ailleurs également appelés pour cette raison, coûts proportionnels.

L’hypothèse de proportionnalité est acceptable sous les conditions suivantes, qui posent autant de limites au modèle[1] :

• les tarifs des fournisseurs de matières premières et autres fournitures sont censés varier proportionnellement aux quantités. En réalité, on se doute que cela n’est guère vrai, car les fournisseurs proposent généralement des tarifs dégressifs ;
• les frais d’approvisionnement sont également censés être proportionnels en fonction des quantités transportées. Mais, il est rare, là aussi, que ne soient pas accordés des tarifs dégressifs[2]. Enfin, la variabilité des charges peut dépendre quelquefois, autant du kilométrage parcouru que des quantités transportées…
• on suppose nuls ou presque les effets de la courbe d’apprentissage. Il s’agit là d’une hypothèse d’école, car ceux-ci sont généralement bien réels et peuvent avoir un impact sur le volume des matières premières utilisés, de la main-d’œuvre, voire sur les coûts d’organisation ;
• enfin, on suppose nuls les stocks en raison d’une part, des variations possibles de valeur d’une période à l’autre et d’autre part, du problème posé par l’existence de produits non encore vendus : toutes les quantités produites ou achetées sont donc censées être vendues.

A ces diverses conditions, qui concernent uniquement les coûts variables, on peut en ajouter deux autres :

• la première tient au fait que les tarifs de vente aux clients ne sont pas, eux non plus, fixes à l’unité. De fait, si l’entreprise ne vend pas exclusivement au détail et sans distinction à l’égard de ses clients, elle sera elle aussi, amenée à pratiquer des tarifs dégressifs. Ceci modifiera par conséquent son chiffre d’affaires et par là même les conditions de calcul de son seuil de rentabilité ;
• la seconde remarque porte sur les frais fixes. Outre que ces derniers ne sont pas forcément fixes en raison des variations de coût toujours possibles dans l’absolu, ils évoluent généralement par paliers. Aussi, lorsque l’on franchit un certain seuil de chiffre d’affaires, on peut s’attendre pour une quantité donnée de produits fabriqués, à passer à un niveau supérieur de frais fixes, ce qui là aussi, modifie les conditions de calcul du modèle.

Ces différentes précisions apportées, il faut cependant garder à l’esprit que les calculs n’ont pas toujours besoin d’être précis au centime près dans la réalité. Ce qui importe est la visibilité fournie par le modèle lors de l’établissement de prévisions. A moins qu’une des conditions énoncées plus haut ait réellement un poids important, auquel cas il conviendra de tenir compte de son impact dans les calculs, le modèle est valable grosso modo.

Il est maintenant possible de décrire le modèle du seuil de rentabilité, appelé aussi parfois modèle « coûts-profit-volume ».

2.  Coûts variables et seuil de rentabilité

Le seuil de rentabilité est une notion relativement aisée à comprendre. Il peut cependant être calculé de différentes manières. C’est pourquoi, il est nécessaire de bien préciser quelques définitions au préalable, avant d’envisager ses extensions sous la forme d’indicateurs de risque.

2.1. Définitions

Schématiquement, le chiffre d’affaires recouvre des coûts variables, des coûts fixes et le résultat.  La différence entre le chiffre d’affaires et les seuls coûts variables donne la « marge » (c’est-à-dire la différence) sur coûts variables. Si cette dernière est supérieure aux coûts fixes, elle laisse un bénéfice, comme on peut le constater sur le schéma suivant :

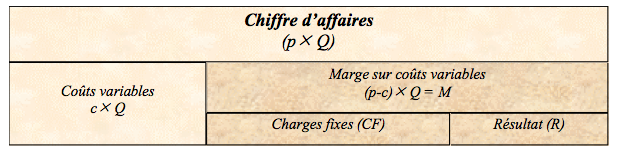
Figure 2.1-1. : le chiffre d’affaires et ses composantes

Les abréviations ont les significations suivantes :

• p = prix unitaire
• c = coût variable unitaire
• M = marge sur coûts variables totale
• m = marge sur coût variable unitaire ; m est égal à : p – c
• CA = chiffre d’affaires
• Q = quantités produites et vendues
• CF = coûts fixes
• R = résultat

Dans le modèle du seuil de rentabilité, on cherche à déterminer le point à partir duquel les charges fixes sont couvertes, ce qui correspond au moment où l’on va commencer à dégager du profit. A partir de l’équation de résultat (différence entre produits et charges variables et fixes) :

On peut en déduire que le seuil de rentabilité (exprimé en quantités) est atteint lorsque les coûts fixes sont couverts par la marge sur coûts variables totale, c’est-à-dire encore, lorsque le résultat, de négatif, devient nul pour basculer en positif, d’où :

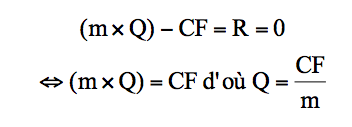
Dans cette expression, les quantités au seuil de rentabilité (on parle aussi de « point mort ») sont mesurées par le rapport entre les coûts fixes et la marge sur coût variable unitaire.

✍ La société de conseil, « Sigma Conseil » vend des séminaires à une clientèle d’entreprises. Chaque séminaire entraîne deux catégories de coûts, fixes et variables qui peuvent être différentes selon le thème du séminaire. On se propose de monter une journée sur le management par activité pour laquelle ont été recensées :

• des charges fixes, pour un montant de 1 000 € par jour représentées par le coût de l’animateur et la location de la salle ;
• des charges variables pour une valeur de 30 € par participant, constituées du coût des repas et des supports de cours fournis.

Le prix de vente d’un séminaire est de 100 € par jour.

Les dirigeants s’interrogent sur la rentabilité de l’opération. Un associé chargé d’étudier l’opération a résumé le problème sous divers angles. Il en donne ci-après une représentation, en fonction des quantités :

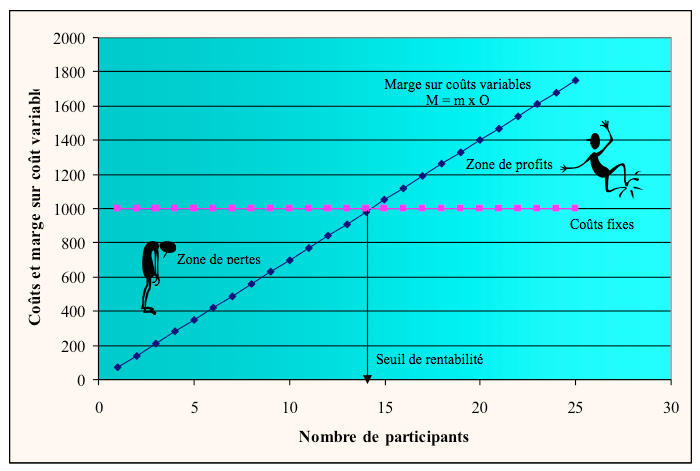
Figure 1.2‑1 : le seuil de rentabilité exprimé en fonction des quantités

Au seuil de rentabilité, on constate ainsi qu’il faut au moins 15 personnes (à 14 personnes on est encore sous le seuil de rentabilité) pour que le séminaire commence à être rentable ; c’est-à-dire encore, un chiffre d’affaires de :

15 × 100 = 1 500 €

Cette expression peut être traduite directement en fonction du chiffre d’affaires. Il suffit pour cela, d’appliquer un taux de marge (noté « t ») au prix de vente. La démonstration ci-après donne la formule du seuil de rentabilité en chiffre d’affaires, en partant de la formule du seuil de rentabilité en quantité :

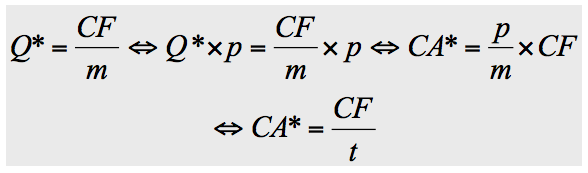
☞ Le taux de marge d’un produit représente le rapport entre la marge sur coûts variables et le chiffre d’affaires (ou la marge sur coût variable et le prix de vente unitaire).

Le taux de marge exprime ainsi, le pourcentage du prix de vente qui reste à l’entreprise après avoir tenu compte des coûts variables. Dès lors, la marge sur coûts variables totale est égale à :

M =  t × CA, d’où :

✍ La société « Sigma Conseil » dégage un taux de marge égal à :

100 – 30 = 70 €, soit : 70/100 = 70 %

Le chiffre d’affaires au seuil de rentabilité est :

CA = 1 000/0,70 = 1 428,57 €

Que l’on est obligé d’arrondir à 1 500 €  pour 15 personnes.

Il faut ajouter à ces deux modes de calcul, que l’on peut aussi déterminer la date à laquelle le seuil de rentabilité est atteint. Il suffit pour cela, d’examiner la progression du chiffre d’affaires ou des ventes au cours d’une période observée et de les situer dans le temps.

Compte tenu de ces différentes approches, on peut finalement dire que :

☞ Le seuil de rentabilité se définit comme le point à partir duquel la marge sur coûts variables couvre les charges fixes. Ce point peut être exprimé sous forme de quantités, de chiffre d’affaires ou d’une date.

2.2. Seuil de rentabilité et indicateurs de gestion

Plusieurs indicateurs peuvent être tirés du modèle de seuil de rentabilité, qui permettent d’avoir une estimation relative du risque. Nous nous contenterons ici, de présenter ceux calculés simplement, à partir du seuil de rentabilité. Dans tous les cas de figure, nous proposons des « formules » permettant de calculer rapidement les résultats recherchés.

a) La marge de sécurité

☞ La marge de sécurité (notée MS) se définit étant comme la différence entre le chiffre d’affaires annuel et le seuil de rentabilité (noté SR) exprimé en chiffre d’affaires (noté CA), soit :

MS = CA - SR

Autrement dit, la marge de sécurité représente le montant de chiffre d’affaires qui peut éventuellement être supprimé pour quelque raison que ce soit, sans entraîner de perte pour l’entreprise.

⚐ La marge de sécurité peut également être calculée d’une autre manière. En effet :

La marge de sécurité peut aussi être appréciée de manière relative, à travers l’indice de sécurité.

b) L’indice de sécurité

Si l’on rapporte la marge de sécurité au chiffre d’affaires global, on obtient un « indice de sécurité » (noté IS), soit :

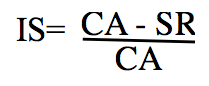
☞ L’indice de sécurité représente le pourcentage de chiffre d’affaires qui peut être supprimé sans entraîner de pertes pour l’entreprise.

⚐ De la même manière que pour la marge de sécurité, il est possible de calculer l’indice de sécurité à partir du résultat. En reprenant l’expression simplifiée de MS, on obtient :

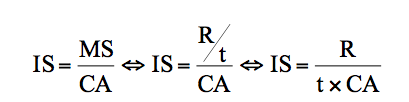
or, t × CA représente la marge sur coûts variables (M), d'où :

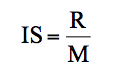
Une autre formulation est également envisageable :

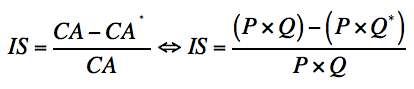
En simplifiant par P, le prix unitaire, on obtient :

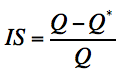
L’une ou l’autre expression sera employée suivant le contexte du problème.

c) L’indice de prélèvement

☞ L’indice de prélèvement (noté IP) représente le pourcentage de chiffre d’affaires permettant de couvrir les charges fixes, soit :

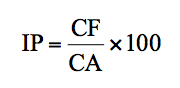
Il est évident que plus cet indice sera élevé, c’est-à-dire proche de 1, plus il sera difficile d’atteindre le seuil de rentabilité. Au-delà de 1, il vaut évidemment mieux renoncer…

2.3. Le coefficient de volatilité, ou levier opérationnel (LO)

☞ Le levier opérationnel exprime le pourcentage de variation du résultat obtenu, pour une variation en pourcentage du chiffre d’affaires.

✏ Un levier opérationnel de + 1,5 pour une augmentation de 10 % du chiffre d’affaires entraîne  une variation corrélative du résultat de : LO x 1,5 % = 15 %.

Le levier opérationnel représente en réalité l’élasticité du résultat par rapport au chiffre d’affaires, d’où son nom de coefficient de volatilité. L’élasticité est exprimée par le rapport entre le coefficient de variation d’un terme et le coefficient de variation d’un autre terme. Un simple taux de croissance est un coefficient de variation. Ainsi l’élasticité des prix par rapport aux quantités est mesurée par le rapport entre le taux de croissance des prix et celui des quantités. On observe ainsi que pour des produits de consommation courante, l’élasticité est négative : en effet, si on diminue le prix d’un bien commun, les consommateurs auront tendance à acheter plus de ce produit, au détriment de la concurrence probablement. Le prix et les quantités évoluent par conséquent en sens inverse.

⚐ On note que l’expression de l’élasticité du résultat par rapport au chiffre d’affaires, le coefficient de volatilité, peut se simplifier, comme on peut le constater (« e » désigne l’élasticité et D une différence) :

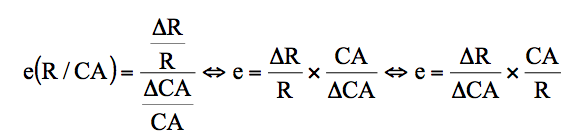
or
et de plus :
donc
d'où :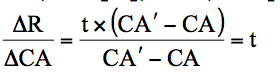
Ce qui revient à dire que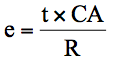
ou encore :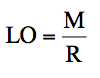

⚐ On note au passage que le calcul simplifié du levier opérationnel aboutit à un rapport inverse de l’indice de sécurité. On pourra donc aisément retrouver l’un ou l’autre en prenant l’inverse du chiffre calculé.

Le levier opérationnel présente un grand intérêt, car il permet, pour un résultat donné, d’obtenir immédiatement la répercussion d’une variation du chiffre d’affaires sur ce résultat. Comment s’explique que la variation du second puisse être plus que proportionnelle à celle du premier ? La raison tient à l’existence de coûts fixes. En effet, ceux-ci étant par définition… fixes, si la marge sur coûts variables globale augmente, le résultat va augmenter d’autant, mais plus que proportionnellement par rapport au chiffre de départ. L’expression simplifiée du levier opérationnel permet en outre, d’effectuer le calcul sans avoir à connaître les variations de chiffre d’affaires et de prix.

Indépendamment de l’exemple présenté plus haut, le levier opérationnel peut être utilisé en de nombreuses circonstances comme l’illustre le cas suivant :

❝ La société Pauline est une entreprise grassoise spécialisée dans la fabrication de flacons de parfum. Elle souhaite plus particulièrement développer l'activité « parfumerie de luxe ». Certes, cette activité paraît beaucoup plus rentable, mais aussi plus risquée : sur 100 lancements par an de parfums, 90 seront abandonnés. La société Pauline subit indirectement ce risque. Par ailleurs, la parfumerie de luxe connaît une fluctuation des ventes très marquée. C’est pourquoi, il est envisagé de modifier une partie de la structure de production pour développer une nouvelle gamme appelée « Zéphir » avec le parfumeur Boyer. La société doit-elle  procéder à cet investissement ? Pour répondre, partiellement, à cette question, il convient de procéder à une analyse du risque d'exploitation de la future structure de production pour les années N et N+1.

Le prix de vente prévu du flacon « Zéphir » est de 180 F. Les investissements généreront 40 800 000 F de frais de structure par an. Les charges variables, quant à elles, représentent 10 % du prix de vente.

Une étude de marché estime la demande moyenne à 300 000 flacons pour la première année (N+1) et à 400 000 pour l’année suivante (N+2). L’effet d’apprentissage devrait limiter les rebuts et par conséquent, autoriser une réduction du coût variable de 10 %.

On calculera les indicateurs suivants :

a. le seuil de rentabilité et le pourcentage des ventes permettant de dégager un bénéfice (c’est-à-dire  l’indice de sécurité) ;

b. le levier d'exploitation.

a. Seuil de rentabilité et indice de sécurité

• Seuil de rentabilité

Marge sur coût variable de l’année N : 180 ×  0,9 = 162 F. Le taux de marge est de 90 % (les coûts variables représentent 10 %).

Seuil de rentabilité année N : 40 800 000/0,90 = 45 333 333 F, ce qui correspond à 45 333 333/180 = 251 851,85, soit : 251 852 flacons.

Marge sur coût variable de l’année N+1 : 180 – (18 ×  0,9) = 163,80 F. Le taux de marge  est de : 163,80/180 = 91 %.

Seuil de rentabilité année N+1 : 40 800 000/0,91 = 44 835 165 F, ce qui correspond à 44 835 165/180 = 249 084,25 soit : 249 085 flacons.

• Indice de sécurité

Année N : (300 000 – 251 852)/300 000 = 16,05 %

Année N+1 : (400 000 – 249 085)/400 000 = 37,72 %

On notera que le calcul peut s’effectuer directement à partir des quantités, puisque le prix demeure uniformément de 180 F.

b. Levier d’exploitation

Année N : la version abrégée du levier d’exploitation est : M/R. Mais, on observe par ailleurs que la version simplifiée de l’indice de sécurité est elle-même égale à : R/M. D’où il ressort que le levier d’exploitation représente l’inverse de l’indice de sécurité. Par conséquent, LO = 1/IS = 1/0,1605 = 6,23.

Année N+1 : LO = 1/0,3772 = 2,65

La conclusion que l’on peut tirer de ces différents calculs est de manière générale, que le risque est nettement moins élevé la deuxième année que la première. En particulier, la réactivité du résultat par rapport au chiffre d’affaires est significativement plus faible en N+1, puisque le levier opérationnel est près de deux fois moins élevé. Ces calculs seront utilement complétés par une mesure de la dispersion du risque (cf. section 2, B. du présent chapitre).

Les instruments décrits dans cette section permettent de répondre à de nombreuses questions, mais la réalité est généralement plus complexe que celle décrite dans les modèles et il est donc nécessaire de prévoir des adaptations, voire développer d’autres aspects du modèle. Ce sera l’objet de la deuxième section.

[1] L’existence de ces conditions explique que nous préférions utiliser l’expression « coûts variables » plutôt que « coûts proportionnels », ces derniers constituant un cas de figure idéal, mais peu réaliste.

[2] De manière très triviale, il suffit pour s’en convaincre, de regarder les tarifs de la poste en fonction du poids. Heureusement, le prix n’est pas strictement proportionnel !

Avez-vous tout retenu ? Passons à l'entrainement :