plan de la leçon :
1. L'imputation rationnelle des charges fixes : principes et fondements. 1
1.1 Fondements théoriques et techniques de l'imputation rationnelle. 2
1.2 Élimination de l'influence de l'activité sur les coûts. 4
2. Mise en œuvre de la méthode de l'imputation rationnelle. 6
Exposé :
Nous avons vu dans la leçon 4, de quelle manière se comportaient les différents coûts, variables et fixes, à l'unité et au total. Nous avons également vu dans la leçon 5, comment prendre en compte les charges fixes dans le calcul du coût des produits. Mais, se pose néanmoins le problème suivant : dans la comptabilité analytique par centres d'analyse, les coûts fixes sont imputés aux produits proportionnellement à une clé de répartition (au niveau de la répartition primaire) et d'une clé d'analyse (au niveau de la répartition secondaire). Or, il suffit que l'activité varie pour que le coût soit imputé de manière différente sur les produits. Ce problème est en partie résolu grâce à la mise en œuvre de la méthode de l'imputation rationnelle. Il vous est proposé d'étudier d'abord, quels sont ses fondements théoriques et techniques, avant d'aborder un exemple développé de mise en œuvre.
1. L'imputation rationnelle des charges fixes : principes et fondements
Pour bien comprendre le problème, imaginons la situation suivante :
✍ Dans une entreprise, les charges du centre distribution sont affectées aux produits en fonction du nombre de produits vendus, soit 50 X et 100 Y en période 1. Le montant de ce centre est de 9 000 €. En période 2, il est vendu 60 X et 90 Y. Autrement dit, l'activité concernant le produit X a augmenté et inversement pour le produit Y. Le résultat de cette variation va se traduire par la répartition des charges de la manière suivante :
| Centre de distribution (extrait du tableau de répartition) | ||||
|---|---|---|---|---|
|
Répartition secondaire |
9 000 € |
|||
|
Période 1 |
Période 2 |
|||
|
Produit X |
Produit Y |
Produit X |
Produit Y |
|
|
Quantités vendues |
50 |
100 |
60 |
90 |
|
Charges imputées |
9000 x (50/150) = 3 000 |
9000 x (100/150) = 6 000 |
9000 x (60/150) = 3 600 |
9000 x (90/150)= = 5 400 |
|
Coût unitaire |
60 |
60 |
60 |
60 |
Comme on peut le constater en période 2, le coût global des produits Y a donc augmenté. En d'autres termes, suivant le niveau d'activité, le coût des produits varie (ce qui n'est qu'un simple rappel).
Le principe sur lequel repose la technique de l'imputation rationnelle et précisément d'éliminer l'influence de l'activité sur les coûts. Pour cela, il est nécessaire d'en comprendre les fondements avoir d'étudier la technique de base.
1.1 Fondements théoriques et techniques de l'imputation rationnelle
Les fondements de la méthode répondent à des critiques de fond, que pose le coût complet, quelle que soit la manière dont il est calculé. Pour cette raison, il est important de bien intégrer les objectifs de la méthode et son principe.
1.1.1 Objectifs
Les objectifs sont nés d'un certain nombre de constats dont le tout premier est très paradoxal : lorsque les quantités produites sont faibles, le coût unitaire est plus élevé du fait de l'imputation des charges fixes. Or, ce phénomène est la plupart du temps, lié à un contexte concurrentiel extrêmement rude. Du coup, si on majore le coût du produit et si le prix de vente est déterminé sur la base du coût de revient… le prix va alors augmenter, alors même qu'il s'agit déjà d'un handicap !
Un deuxième constat vient de ce que les coûts fixes représentent bien souvent, une forme d'investissement de capacité : si une machine est capable de produire 100 000 unités et que l'on en fabrique seulement 80 000, il y a donc un potentiel de 20 000 unités. Le non-emploi de cette capacité correspond à une sorte de gaspillage qu'il est utile de chiffrer : ce sont les coûts de sous-activité, que met en évidence l'imputation rationnelle.
Enfin, lorsque l'on calcule sur plusieurs périodes un coût complet unitaire par la méthode des centres d'analyse, celui-ci est susceptible de varier sans qu'il soit toujours possible d'en identifier clairement la cause. La variation de l'activité peut évidemment en être responsable, du seul fait des économies d'échelle, puisqu'elle se traduit par une variation du coût fixe unitaire. Mais, il peut arriver dans certains cas, que cette variation soit aussi imputable aux coûts variables unitaires. C'est donc l'objet de l'imputation rationnelle que d'éliminer l'influence de l'activité sur les coûts et de déterminer les causes réelles de leur variation.
1.1.2 Principe
Le principe sur lequel se fonde l'imputation rationnelle est de rendre « variables » les charges fixes. Plus précisément, il ne s'agit pas d'en modifier la nature – de rendre variables des charges fixes – mais de traiter ces dernières comme des charges variables, sachant qu'il apparaîtra automatiquement un écart par ailleurs. L'exemple de la société « Toutenbois » qui suit, va permettre de comprendre le problème :
✍ Un produit est fabriqué à l'aide d'une seule matière première, le bois, et est transformé dans un atelier. Il est donc composé d'un coût variable direct, le bois, et d'un coût provenant de l'atelier, imputé sur la base des heures machine.
Il a été fabriqué 10 000 unités au cours du mois de janvier, et 12 000 en février. La matière première revient à 50 € par unité. Les frais de centre sont de 95 000 €, dont 60 000 € de frais fixes. Le coût unitaire par produit et par mois est donc de :
|
Janvier |
Février |
|
|---|---|---|
| Charges directes |
500 000 |
600 000 |
Charges de centre :
|
35 000 60 000 |
42 000 60 000 |
| Total |
595 000 |
702 000 |
| Quantités produites |
10 000 |
12 000 |
Coût unitaire
|
59,50 53,50 6,00 |
58,50 53,50 5,00 |
Les charges variables pour le mois de février ont été calculées proportionnellement aux quantités fabriquées, soit : 35 000 × (12 000/10 000) = 42 000 €.
On voit dans cet exemple, qu'à partir du moment où les charges fixes ne sont pas modifiées, alors que l'activité varie en fonction des quantités de chaises fabriquées d'un mois sur l'autre, le coût unitaire complet varie également. Comment éviter cet écueil ?
1.2 Élimination de l'influence de l'activité sur les coûts
Afin de mettre en œuvre la méthode, il est nécessaire au préalable de définir deux notions : l'activité normale et le coefficient d'imputation rationnelle.
☞ L'activité normale correspond à l'activité ordinaire de la firme dans des conditions normales ou habituelles de fonctionnement. Il s'agit d'un niveau de référence.
☞ Le coefficient d'imputation rationnelle représente le rapport entre l'activité réelle (Ar) et l'activité normale (An). Il sert à imputer les charges fixes dans le calcul des coûts.
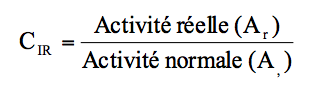
Ce rapport signifie que si l'activité réelle est supérieure à la normale, il conviendra d'affecter un surcroît de charges fixes au coût du produit et inversement, si l'activité réelle est inférieure à la normale, on diminuera le montant des charges fixes. Ce principe est illustré par l'exemple suivant :
✍ On considère que l'activité normale pour la société Toutenbois est de 10 000 unités par mois. L'application des coefficients d'imputation rationnelle permet de garder un coût unitaire du produit identique quel que soit le niveau d'activité, comme le montre le tableau suivant :
|
Sous-activité |
Activité normale |
Suractivité |
||||
|---|---|---|---|---|---|---|
|
Production |
8 000 |
Imputation des charges fixes |
10 000 |
Imputation des charges fixes |
12 000 |
Imputation des charges fixes |
|
Coefficient d'IR |
0,80 |
1 |
1,2 |
|||
|
Charges directes |
400 000 |
500 000 |
600 000 |
|||
|
Charges de centre :
|
28 000 48 000 |
60 000 × 0,80 = 48 000 |
35 000 60 000 |
60 000 × 1 = 60 000 |
42 000 72 000 |
60 000 × 1,20 = 72 000 |
|
Total |
476 000 |
595 000 |
714 000 |
|||
|
Coût unitaire
|
59,50 53,50 6,00 |
Ecart d'imputa-tion 12 000 |
59,50 53,50 6,00 |
59,50 53,50 6,00 |
Ecart d'imputa-tion - 12 000 |
|
La « variabilisation » des charges fixes ne signifie pas qu'une partie d'entre elles est supprimée. Les écarts demeurent en réalité dans l'entreprise et dans ses comptes, mais ils apparaissent sous forme « d'écarts d'imputation ».
Si l'écart est négatif, autrement dit, que les charges imputées rationnellement sont supérieures aux charges réelles, on parlera de « boni de suractivité » pour signifier que l'appareil de production a dégagé un surcroît d'activité. En même temps, ce boni traduit le fait – s'il est récurrent – que l'investissement initial dans l'appareil de production a été insuffisant : il faut s'interroger sur le point de savoir si l'on ne devrait pas augmenter les capacités normales de production. A l'inverse, si les charges imputées rationnellement sont inférieures aux charges réelles, on parlera de « coût de sous-activité » pour signifier qu'une part des charges fixes n'a pu être absorbée par l'activité réelle. Dans ce cas, et à nouveau si l'écart est récurrent, cela peut signifier que l'entreprise a investi à l'origine dans une surcapacité de production. A l'issue de la période, les écarts d'activité se compensent, pour ne laisser qu'un écart résiduel d'imputation rationnelle, correspondant au boni de suractivité ou au coût de sous-activité pour l'année ou l'exercice.
L'intérêt de la méthode est de permettre, en isolant la part de variabilité du coût fixe unitaire lié au niveau d'activité (du fait des économies – ou des déséconomies – d'échelle sur frais fixes), de contrôler les performances réelles au niveau des charges variables de centre.
✍ La société Toutenbois possède les données réelles suivantes pour le mois de mars :
|
Activité normale |
Activité réelle |
|||
|---|---|---|---|---|
|
Niveau d'activité |
10 000 |
Imputation des charges fixes |
12 000 |
Imputation des charges fixes |
|
Coefficient d'IR |
1 |
1,2 |
||
|
Charges directes |
500 000 |
600 000 |
||
|
Charges de centre :
|
35 000 60 000 |
60 000 × 1 |
48 000 72 000 |
60 000 × 1,20 |
|
Total |
595 000 |
720 000 |
||
|
Coût unitaire
|
59,50 53,50 6,00 |
60,00 54,00 6,00 |
Ecart d'imputation - 12 000 |
|
Dans cet exemple, il apparaît à la lecture du tableau que les charges variables de centre, loin d'être proportionnelles aux quantités, ont été en réalité supérieures à ce qui était prévisible. On va donc pouvoir chercher à comprendre l'origine de cet écart, qui ne serait pas ressorti de manière évidente, si l'on n'avait pas mis en œuvre la technique de l'imputation rationnelle. Une des causes peut être, par exemple, l'augmentation du coût de l'énergie dans l'atelier.
Cet exemple simple ne permet pas cependant, de donner une image complète du processus. Aussi, une illustration complète est présentée dans le paragraphe suivant.
2. Mise en œuvre de la méthode de l'imputation rationnelle
La mise en œuvre est présentée à travers un cas. Sont d'abord exposées les données du problème, puis la solution est présentée. Le plan adopté pour cette partie correspond aux étapes essentielles qui permettent de mettre en œuvre la méthode.
2.1. Données du problème
✍ La Société Métallurgique de Lorraine est une société anonyme implantée dans l'Est de la France. Elle emploie 592 personnes dont 495 dans deux ateliers :
- l'atelier de calibrage qui effectue des opérations de calibrage de barres et de couronnes d'acier brut ;
- l'atelier de barres de torsion où sont réalisés des produits finis pour l'automobile à partir des barres précédemment calibrées.
La SMT n'achète pas ses matières premières et n'a pas de service commercial, car elle sous-traite toute sa production à une filiale du groupe auquel elle appartient. Pour la répartition de ses charges indirectes, la société a déterminé cinq centres d'analyse correspondant à un regroupement de ses services :
- le centre d'analyse administration ;
- le centre d'analyse entretien ;
- le centre d'analyse approvisionnements ;
- les centre d'analyse atelier de calibrage et atelier de barres de torsion.
Pour le mois de janvier N, il a été décidé d'utiliser la méthode de l'imputation rationnelle des charges fixes.
Il a été relevé au cours du mois de janvier N, les informations suivantes :
-
charges directes : il s'agit de la main‑d'œuvre rémunérée :
- atelier de calibrage : 38 570 heures pour 1 149 386 € ;
- atelier des barres de torsion : 15 080 heures pour 470 496 €.
- L'unité d'œuvre utilisée pour chaque atelier est l'heure de marche.
| Tableau de répartition | ||||||
|---|---|---|---|---|---|---|
| Eléments | TOTAL | Centres d'analyse auxiliaires | Centres d'analyse principaux | |||
| Adminis-tration | Entretien | Approvision-nement | Calibrage | Barres de torsion | ||
| Achats stockés de mat. premières |
322 301 |
322 301 |
||||
| Charges de personnel |
821 128 |
318 624 |
146 158 |
138 256 |
161 575 |
56 515 |
| Impôts et taxes |
14 206 |
9 565 |
1 082 |
950 |
1 438 |
1 171 |
| Achats non stockés de mat. et fournitures |
772 628 |
128 642 |
341 231 |
97 228 |
123 386 |
82 141 |
| Transports |
143 527 |
32 121 |
28 634 |
46 652 |
23 572 |
12 548 |
| Services extérieurs |
67 435 |
24 212 |
18 917 |
6 432 |
12 488 |
5 386 |
| Charges financières |
46 222 |
46 222 |
||||
| Dotations aux amortissements |
1 100 900 |
59 098 |
114 673 |
28 421 |
682 218 |
216 490 |
| Totaux répartition primaire |
3 288 347 |
618 484 |
650 695 |
640 240 |
1 004 677 |
374 251 |
| Administration |
75 % |
25 % |
||||
| Entretien |
10 % |
75 % |
15 % |
|||
| Approvision-nement |
5 % |
65 % |
30 % |
|||
| Totaux |
3 288 347 |
0 |
0 |
– |
– |
– |
Une analyse très poussée des charges indirectes du mois de janvier N a permis d'obtenir dès le mois suivant la répartition ci‑après :
-
Frais variables :
- 100 % des achats stockés de matières,
- 40 % des achats non stockés de matières et fournitures,
- 70 % des transports 50 % des services extérieurs.
- frais fixes : le reste des charges indirectes.
L'atelier de calibrage a produit au cours de ce mois de janvier N, 306 254 barres et 246 564 couronnes. Il est admis que l'ensemble des charges nécessaires au calibrage d'une couronne est égal à une fois et demie celle du calibrage d'une barre. L'atelier de barres de torsion a produit 175 264 barres dont 1 366 ont été mise au rebut ; elles seront reprises par les fournisseurs sans contrepartie.
L'analyse de l'activité de la société a permis de déterminer les coefficients d'imputation rationnelle pour le mois de janvier N suivants :
- Centre Administration : 1
- Centre Entretien : 0,9
- Centre Méthodes et approvisionnement : 1
En ce qui concerne les centres d'analyse principaux, L'activité considérée comme normale est de :
- atelier de calibrage : 36 400 heures de marche,
- atelier des barres de torsion : 16 250 heures de marche.
La démarche à suivre est formalisée dans les étapes a) à c), la dernière correspondant au calcul du coût de revient :
a) Calculer les coefficients d'imputation rationnelle des centres principaux pour le mois de janvier N.
b) Procéder à la répartition primaire des charges indirectes en séparant pour chaque centre d'analyse, la partie fixe et la partie variable.
c) Calculer par la méthode d'imputation rationnelle le coût de l'unité d'œuvre des centres d'analyse de calibrage et de barres de torsion, ainsi que l'écart global d'imputation rationnelle.
d) Calculer le coût du calibrage d'une barre et d'une couronne, ainsi que le coût de la fabrication d'une barre de torsion utile.
A noter : tous les calculs sont réalisés sur Excel. Les valeurs sont donc exactes.
2.2. Démarche à suivre
a) Calcul des coefficients d'imputation pour le mois de janvier N
Seuls les coefficients d'imputation rationnelle des centres principaux nécessitent un calcul, puisque ceux des centres auxiliaires sont donnés.
✍ Atelier calibrage :
- Activité réelle : 38 570
- Activité normale : 36 400
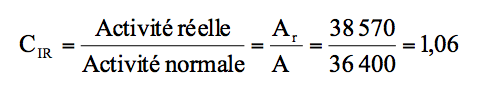
Atelier barres de torsion :
- Activité réelle : 15 080
- Activité normale : 16 250
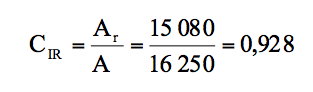
b) Répartition des charges indirectes
✍ La répartition des charges indirectes est réalisée en distinguant les charges fixes, des charges variables. L'ensemble des calculs est résumé dans le tableau ci-après :
| TABLEAU DE RÉPARTITION | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Eléments | Centres d'analyse auxiliaires | Centres d'analyse principaux | |||||||||
| Totaux | Administration | Entretien | Méthodes et approvt. | Calibrage | Barres de torsion | ||||||
| Var. | Fixe | Var. | Fixe | Var. | Fixe | Var. | Fixe | Var. | Fixe | ||
| Matières premières |
322 301 |
322 301 |
|||||||||
| Charges de personnel |
821 128 |
318 624 |
146 158 |
138 256 |
161 575 |
56 515 |
|||||
| Impôts et taxes |
14 206 |
9 565 |
1 082 |
950 |
1 438 |
1 171 |
|||||
| Achats non stockés |
772 628 |
51 457 |
77 185 |
136 492 |
204 739 |
38 891 |
58 337 |
49 354 |
74 032 |
32 856 |
49 285 |
| Transports |
143 527 |
22 485 |
9 636 |
20 044 |
8 590 |
32 656 |
13 996 |
16 500 |
7 072 |
8 784 |
3 764 |
| Services extérieurs |
67 435 |
12 106 |
12 106 |
9 459 |
9 459 |
3 216 |
3 216 |
6 244 |
6 244 |
2 693 |
2 693 |
| Charges financières |
46 222 |
46 222 |
|||||||||
| Dotations |
1 100 900 |
59 098 |
114 673 |
28 421 |
682 218 |
216 490 |
|||||
| Répartition primaire |
3 288 347 |
86 048 |
532 437 |
165 995 |
484 700 |
397 065 |
243 175 |
72 099 |
932 578 |
44 333 |
329 918 |
c) Détermination du coût des unités d'œuvre avec imputation rationnelle
L'imputation rationnelle est menée en application des principes énoncés plus haut. Les charges fixes sont ainsi multipliées par les coefficients. La différence entre les charges fixes calculées et les charges fixes réelles est reportée en fin de tableau. L'écart positif final (16 628) indique un coût de sous-activité, puisqu'une partie des charges fixes correspondant à l'activité normale n'a pu être imputée au coût des produits. Ces calculs sont résumés dans le tableau ci-après, en même temps que sont repris les résultats précédents.
| TABLEAU DE REPARTITION | Différence d'imputation | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eléments | Totaux | Centres d'analyse auxiliaires | Centres d'analyse principaux | ||||||||||
| Administration | Entretien | Méthodes | Calibrage | Barres de torsion | |||||||||
| Variable | Fixe | Variable | Fixe | Variable | Fixe | Variable | Fixe | Variable | Fixe | Positive | Négative | ||
|
Matières premières |
322 301 |
322 301 |
|||||||||||
|
Charges de personnel |
821 128 |
318 624 |
146 158 |
138 256 |
161 575 |
56 515 |
|||||||
|
Impôts et taxes |
14 206 |
9 565 |
1 082 |
950 |
1 438 |
1 171 |
|||||||
|
Achats non stockés |
772 628 |
51 457 |
77 185 |
136 492 |
204 739 |
38 891 |
58 337 |
49 354 |
74 032 |
32 856 |
49 285 |
||
|
Transports |
143 527 |
22 485 |
9 636 |
20 044 |
8 590 |
32 656 |
13 996 |
16 500 |
7 072 |
8 784 |
3 764 |
||
|
Services extérieurs |
67 435 |
12 106 |
12 106 |
9 459 |
9 459 |
3 216 |
3 216 |
6 244 |
6 244 |
2 693 |
2 693 |
||
|
Charges financières |
46 222 |
46 222 |
|||||||||||
|
DAP |
1 100 900 |
59 098 |
114 673 |
28 421 |
682 218 |
216 490 |
|||||||
|
Répartition primaire |
3 288 347 |
86 048 |
532 437 |
165 995 |
484 700 |
397 065 |
243 175 |
72 099 |
932 578 |
44 333 |
329 918 |
||
|
CIR |
- |
1 |
- |
0,90 |
- |
1 |
1,06 |
0,93 |
|||||
|
Imputation rationnelle |
532 437 |
436 230 |
243 175 |
988 174 |
306 164 |
||||||||
|
Écart d'IR |
- |
48 470 |
- |
- 55 596 |
23 754 |
72 224 |
- 55 596 |
||||||
|
Total (avec IR) |
618 484 |
602 225 |
640 240 |
1 060 273 |
350 497 |
16 628 |
|||||||
|
Adminis-tration |
- 618 484 |
463 863 |
154 621 |
||||||||||
|
Entretien |
-637 424 |
63 742 |
478 068 |
95 614 |
|||||||||
|
Méthodes |
35 199 |
- 703 982 |
457 588 |
211 195 |
|||||||||
|
Totaux |
3 288 347 |
0 |
0 |
0 |
2 459 792 |
811 926 |
|||||||
|
Nature UO |
L'heure de marche |
L'heure de marche |
|||||||||||
|
Nombre UO |
38570 |
15080 |
|||||||||||
|
Coût UO |
63,77 |
53,84 |
|||||||||||
N.B. – Tous les calculs de ce tableau ont été réalisés sur Excel. Il peut donc apparaître des différences si cet exemple est retraité à l'aide d'une calculette. Cela est vrai notamment pour le coût des unités d'œuvre.
d) Calcul du coût de production d'une barre de torsion et d'une couronne
✍ Sachant qu'une couronne demande un ensemble de charges égal à une fois et demie celles des barres, il est possible (en admettant l'hypothèse de stricte proportionnalité) de traduire l'ensemble des charges en équivalents barres, soit :
| Production janvier | |||
|---|---|---|---|
| Production réelle | Coefficients | Equivalents | |
| Barres |
306 254 |
1 |
306 254 |
| Couronnes |
246 564 |
1,5 |
369 846 |
| Total |
676 100 |
||
Le coût de production des équivalent-barres, à l'issue du premier atelier calibrage est alors :
| Coût de production | Barres |
|---|---|
|
MOD |
1 149 386 |
|
Atelier calibrage |
2 459 792(1) |
|
Coût total |
3 609 178 |
|
Coût unitaire |
5,34 |
(1)Temps de marche, multiplié par le coût d'unité d'œuvre
(2) 3 609 178/676 100 = 5,34
Soit pour une couronne : 5,33823 × 1,5 =8,007
Le coût de production des barres de torsion est :
| Coût de production | Barres de torsion |
|---|---|
| Coût matière |
5,34 |
| Quantité |
175 264 |
| Total |
935 600 |
| MOD |
470 496 |
| Atelier torsion |
811 926 |
| Coût total |
2 218 022 |
| Coût unitaire |
12,75 |
On note que le coût unitaire d'une barre de torsion est calculé sur la base de 175 264 unités diminuées des 1 366 mises au rebut... Ce qui est une manière d'intégrer directement le coût des rebuts dans le coût de production.
Notons que malgré les apports certains de la méthode, celle-ci est relativement peu mise en œuvre dans les entreprises, vraisemblablement en raison de la lourdeur du système et des difficultés posées par l'identification des charges fixes et variables.
