Exposé :

1.  Qu'est-ce qu'un coût ?

La notion de coût est inséparable de l'activité de l'entreprise. Celle-ci vend des marchandises ou des produits manufacturés. Cette activité consomme des ressources (financières, techniques, humaines…) : le chiffrage de ces consommations représente le coût. La définition du coût doit cependant être précisée, car elle a évolué dans le temps et ses limites doivent être posées.

1.1. Définitions

Pour comprendre ce qu'est un coût et ce à quoi il sert, considérons l'exemple suivant :

✍ Habitant Nice, vous avez besoin d'acheter des éléments de bibliothèque que vous ne trouverez que dans une grande surface située à Toulon ou à Marseille. La première ville est distante de 140 km et la seconde, distante de 180 km. L'autoroute revient à 16 € pour la première et à 20 € pour la seconde. Votre voiture consomme 10 l aux 100 à 1 € le litre. Toutefois, les prix pratiqués à Marseille sont en moyenne inférieurs de 3 % à ceux de Toulon.  Votre bibliothèque revient normalement à 600 € (prix affiché à Toulon). Dans quelle grande surface allez-vous vous rendre ?

Un calcul simple permet de répondre à la question :

	Toulon	Marseille
Prix du trajet
Autoroute	16 €	20 €
Essence	[(140x10)/100] x 1 € = 14 €	[(180x10)/100] x 1 € = 18 €
Coût total de l'achat
Valeur de l'achat	600 €	600 €
Économie sur l'achat	0	600 x 0,03 = 18 €
Coût du transport	16 + 14 = 30 €	20 + 18 = 38 €
Coût d'achat	16 + 14 + 600 = 630 €	20 + 18 + 600 – 18 = 620 €

Bien entendu, cet exemple est simplifié, car il faudrait également prendre en compte l'usure de la voiture (plus grande, si l'on se rend à Marseille), le temps passé (également plus long sur Marseille) et d'autres éléments difficilement chiffrables, tels que les facilités d'accès au parking et/ou l'offre en magasin (peut-être plus conséquente à Marseille)… Mais, on constate que le calcul de coût permet d'aider à prendre une décision. Il passe par le recensement des frais engagés dans l'opération et la comparaison coût/avantages procurés par l'opération.

☞ Un coût peut être défini comme la somme des charges relatives à un élément (produit, activité, fonction…).

Cette définition revient à dire que le coût est constitué de l'ensemble des frais engagés dans une opération, de quelque nature qu'elle soit. En règle générale, ces frais sont recensés dans le compte de résultat, d'où l'utilisation du terme de charges.

⚡ Attention ! il ne faut cependant pas considérer un coût comme l'équivalent d'une charge, dont le sens premier signifie « poids », voire « fardeau ». L'assimilation des deux termes peut laisser à penser qu'il n'existe pas d'autres coûts que ceux enregistrés en comptabilité générale (ce qui est faux) et risque de donner l'impression que les coûts sont subits, comme le sont les charges, le travail de l'analyste se réduisant à les imputer aux produits.

Notons aussi, qu'un coût est le fruit d'un calcul, par opposition à un prix qui est le résultat de l'offre et de la demande sur un marché. Il est par conséquent, vivement conseillé d'éviter de parler de « prix de revient » pour désigner les « coûts de revient », expression couramment utilisée dans le langage de l'entreprise.

Enfin, observons que le coût n'est pas unique. Ainsi, l'imputation de l'assurance, par exemple peut se faire au prorata des kilomètres (on suppose alors que l'on parcourt un certain nombre de km en moyenne dans l'année, correspondant à la prime annuelle) ou bien forfaitairement en fonction du nombre de déplacements moyen dans l'année, ce qui ne donne pas forcément le même résultat. Selon les hypothèses de calcul que l'on pose, on n'obtiendra donc pas le même coût.

⚡ Cette remarque est très importante, car elle doit vous faire prendre conscience que la comptabilité n'est pas une science exacte qui aboutirait à un résultat unique. D'une part, les calculs sont relatifs aux hypothèses posées, ce qui signifie que non seulement les résultats peuvent être différents, mais ils peuvent être aussi plus ou moins éloignés d'une certaine « réalité » qu'il est de toutes manières, difficile d'appréhender ; d'autre part, le coût peut aussi évoluer dans le temps en fonction des conditions d'exploitation de l'entreprise. Dans le cas du déplacement, il est évident ainsi, que le fait d'utiliser une voiture différente induit un coût différent.

En reprenant l'exemple en introduction, on peut également définir un coût, en considérant les ressources mises en œuvre pour mener à bien un projet. Ces ressources sont déterminées par les différentes activités qu'il est nécessaire de déployer pour arriver au résultat recherché.

☞ Un coût représente la somme des ressources consommées par les activités nécessaires à la mise en œuvre du processus d'élaboration et d'exploitation d'un produit ou d'un service.

☞ De manière schématique, une activité est un ensemble de tâches effectuées à partir d'une matière première, d'un produit ou d'un service, dont le résultat se traduit par un produit ou un service déterminés.

✍ Scier des planches aboutit, à partir d'un billot de bois, à fournir un produit destiné à une autre activité (l'assemblage, par exemple, pour construire un meuble).

L'intérêt de cette deuxième définition est de mettre l'accent sur le fait que le coût est le résultat d'une activité : il n'existe donc pas en tant que tel. C'est en agissant sur une activité que l'on peut agir sur le coût. A l'opposé, vouloir « réduire les coûts » dans l'absolu, revient concrètement à tenter d'élever la température d'une pièce en chauffant le thermomètre. Un coût doit être pris pour ce qu'il est, c'est-à-dire un instrument de mesure.

1.2. Caractéristiques générales

Le coût se caractérise par trois particularités indépendantes les unes des autres : le champ d'application, le moment du calcul, le contenu.

1.2.1.  Le champ d'application

Celui-ci est extrêmement varié. Il peut s'appliquer à :

• une fonction économique de l'entreprise (approvisionnement, production, distribution, administration) ;
• un moyen d'exploitation (magasin, rayon, usine, atelier, poste de travail) ;
• un objet (produit ou famille de produit, client, fournisseur) ;
• tout centre de responsabilité, c'est-à-dire un des sous-systèmes de l'entreprise pour lequel est défini un objectif mesurable et doté d'une certaine autonomie pour atteindre cet objectif (direction commerciale, chef d'atelier, directeur technique).

1.2.2.  Le moment de calcul

Un coût peut être calculé a posteriori : il s'agira alors d'un coût constaté, que nous qualifierons également de « réel ». Il peut aussi être calculé a priori : on parlera alors de « coût préétabli ».

Les coûts préétablis ont une grande importance pour la gestion prévisionnelle de l'entreprise. Ils peuvent prendre la forme de coûts standards, auquel cas ils constitueront une norme sous la forme d'un objectif à atteindre, d'un minimum à satisfaire, voire d'un idéal. Ils peuvent aussi servir à l'établissement de devis dans les rapports commerciaux avec la clientèle. Ils peuvent enfin, être utiles à l'établissement de budgets prévisionnels.

La comparaison entre les coûts préétablis et les coûts réellement constatés permet de mettre en évidence des écarts, dont l'interprétation permet d'aider à la gestion de la firme.

1.2.3.  Le contenu

Selon que le gestionnaire retient la totalité des coûts dans l'entreprise ou une partie seulement, on obtiendra un coût complet ou un coût partiel. Cet aspect est développé au point 3 de cette leçon.

1.3. Limites à la notion de coût

1.3.1. Le coût ne doit pas être considéré comme un ensemble homogène

Considérer les coûts comme un ensemble homogène revient à considérer que différents fruits et légumes peuvent être présentés à la caisse d'un supermarché réunis dans un même emballage, à la raison que l'unité de mesure commune est le kilogramme. C'est pourtant ce qui est fait en matière de calculs de coûts : les coûts constitués de différents types (cf. point 3), sont exprimés en une seule unité, la monnaie, donnant ainsi l'illusion qu'ils sont homogènes. Rien n'est plus dangereux, car cela revient à laisser accroire par exemple, que si un produit coûte 1 €, alors 100 produits coûteront 100 €. En réalité, du fait de l'existence de coûts fixes et de phénomènes tels que l'apprentissage ou les économies d'échelle, le coût pourra différer sensiblement de 100 €.

1.3.2. Le coût n'est pas la valeur

Une autre critique doit être faite aux coûts : ils ne représentent en rien la valeur d'un produit ou d'une activité. Une illustration simple permet de comprendre cette distorsion : si une entreprise fabrique des vêtements démodés, on peut bien avancer que le coût de ces produits est égal à la somme des charges supportées pour les réaliser, mais la valeur marchande est nulle... la valeur est en définitive déterminée par le marché.

2.  TYPOLOGIE DES COÛTS

On peut distinguer quatre types de coûts, lesquels en se croisant forment quatre sous-catégories. Ces dernières sont à l'origine des principales méthodes de calculs.

2.1. Coûts variables et coûts fixes

2.1.1.  Les coûts variables ou opérationnels

☞ Les coûts variables ou opérationnels sont des coûts constitués seulement par les charges qui varient avec le volume d'activité de l'entreprise (par exemple, les quantités produites et/ou vendues) sans qu'il y ait nécessairement exacte proportionnalité entre la variation des charges et la variation du volume des produits obtenus.

La matière contenue dans un produit fabriqué, les frais de transport, l'emballage, sont des exemples de charges variables.

✍ La fabrication d'une chaise ordinaire requiert 6 € de matières premières (contre-plaqué et acier). Le coût variable pour 100 chaises sera donc de : 6 × 100 = 600 €. Ce rapport, dans la réalité, peut ne pas être strictement proportionnel à partir du moment où l'entreprise obtient par exemple, des remises sur le volume des quantités commandées.

Observons dès à présent, que le coût variable par unité est « fixe », alors que le coût variable total est fonction des quantités vendues : il est donc « variable », comme l'indique la figure 2.1-1.

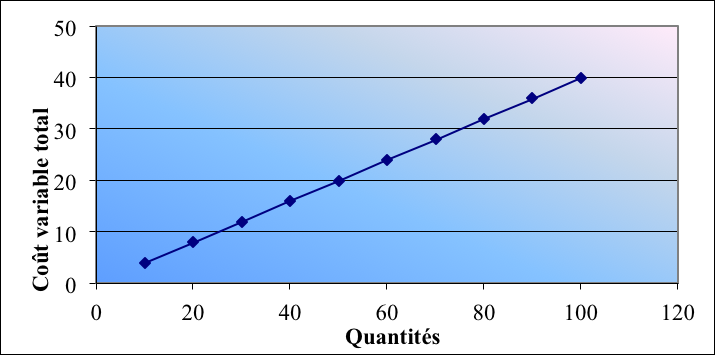
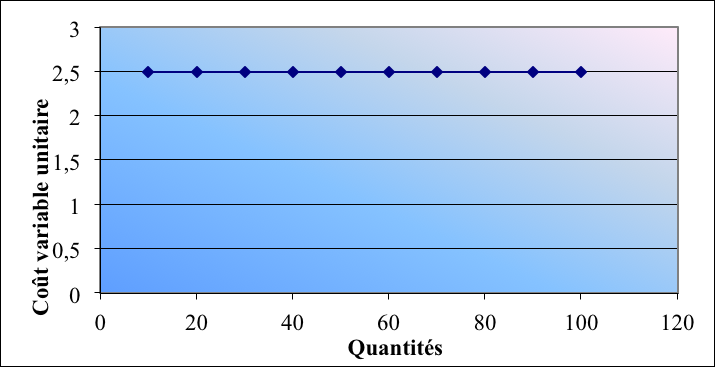
Figure 2.1‑1: évolution comparée du coût variable total et du coût variable unitaire en fonction des quantités

Il faut cependant bien garder à l'esprit que ces schémas sont théoriques, dans la mesure où le coût variable peut ne pas être strictement proportionnel aux quantités produites. Il l'est d'ailleurs rarement dans la réalité et cela explique pourquoi les termes de « coûts proportionnels » ne sont pas pertinents.

2.1.2.  Les coûts fixes ou charges de structure

☞ Ce sont les charges liées à l'existence de l'entreprise et correspondant, pour chaque période de calcul, à une capacité de production déterminée. L'évolution de ces charges avec le volume d'activité est discontinue. Ces charges sont relativement « fixes » lorsque le niveau d'activité évolue peu au cours de la période de calcul.

Les coûts fixes correspondent aux charges engendrées par l'administration ou les investissements durables. Ils ne sont pas proportionnels aux quantités fabriquées.

✍ Le matériel acquis pour fabriquer les chaises a coûté 200 000 €. Il est amorti sur cinq ans en linéaire, ce qui correspond à l'usure économique du bien. Chaque année, on impute 1/5^ème de ce coût à celui des produits fabriqués, soit un montant fixe de 40 000 € qui ne varie pas, quelles que soient les quantités produites.

On peut également observer, que si le coût fixe global ne change pas pour la période considérée, il est en revanche variable par unité, comme le montre la figure 2.1-2.

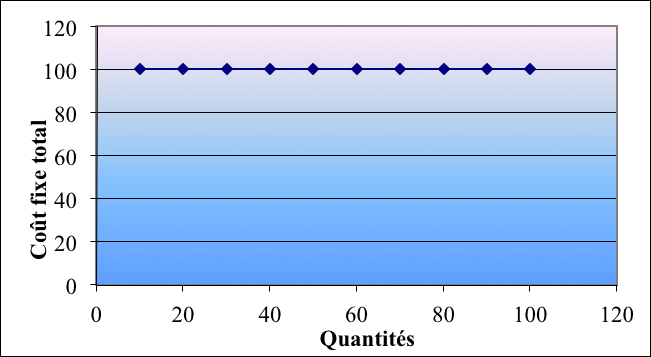
Figure 2.1‑2 : évolution comparée du coût fixe total et du coût fixe unitaire en fonction des quantités

On peut remarquer que l'évolution du coût fixe unitaire prend l'allure d'une hyperbole. Cela s'explique aisément, puisque le coût fixe unitaire représente le rapport entre le coût fixe total et les quantités produites et/ou vendues. Il décroît par conséquent, au fur et à mesure qu'augmentent les quantités produites.

✍ En reprenant les données de l'exemple précédent, si une seule chaise est produite, le coût fixe affecté à celle-ci sera de 40 000 €. Si deux chaises sont produites, ce coût sera de 40 000 / 2 = 20 000 €. Si 20 000 chaises sont produites, ce coût sera de : 40 000/ 20 000 = 2 € par chaise, etc.

2.2. Coûts directs et indirects

☞ Les coûts directs sont ceux qu'il est possible d'affecter immédiatement, c'est-à-dire sans calcul intermédiaire, au coût d'un produit déterminé.

✍ Les matières premières incorporées au produit, les heures de main-d'œuvre des ouvriers affectés à la fabrication du produit, constituent autant de coûts directement imputables aux produits.

Il faut noter que l'affectation de ces coûts dépend toutefois de l'existence de moyens directs de mesure, ce qui explique que les charges les plus communément admises au titre des coûts directs sont les heures de main-d'œuvre et les matières premières. Il ne s'agit cependant pas d'une règle absolue.

☞ Les coûts indirects sont ceux qu'il n'est pas possible d'affecter immédiatement, c'est-à-dire sans calcul intermédiaire, au coût d'un produit déterminé.

✍ Les charges d'administration, les frais généraux d'entretien, de surveillance... sont autant d'exemples de charges indirectes par rapport à l'activité de production.

Les charges indirectes posent un problème important, dans la mesure où leur incorporation au coût du produit nécessite un traitement préalable. Nous verrons comment la méthode des coûts complets, étudiée dans les leçons 4 et 5, traite le problème.

2.3. Synthèse

Ces différentes catégories de coûts peuvent être représentées en définitive sur deux axes, à partir des charges qui les composent déterminant ainsi quatre types bien spécifiques, comme le montre le tableau 2.3-1 :

CHARGES	DIRECTES	INDIRECTES
VARIABLES	Matières premières, frais de distribution, sous-traitance, etc.	Energie (eau, fuel, électricité), petit outillage, fournitures diverses, etc.
FIXES	Main-d'œuvre, dotations aux amortissements des machines affectées à la fabrication des produits, etc.	Personnel administratif, dotations aux amortissements des bâtiments et machines (hors production), etc.

Tableau 2.3‑1 : typologie des charges dans l'entreprise

Il convient à propos de ce tableau, de faire trois observations :

• les charges indiquées dans les différentes cases ne sont indiquées ici qu'à titre indicatif et ne constituent nullement une typologie déterminée et définitive ;
• il n'existe pas toujours de types « purs » de charges : s'agissant des matières premières, il existe par exemple, des tarifs dégressifs en fonction du volume acheté ou transporté. L'électricité n'est pas non plus facturée au même tarif au-delà d'une certaine consommation, ni même au cours d'une journée de 24 h ;
• certaines charges sont mixtes : ainsi en est-il par exemple de l'eau ou du téléphone, qui comprennent un abonnement fixe et un coût variable en fonction de la consommation.

3.  LES DIFFERENTES METHODES DE CALCUL DES COÛTS

L'existence de coûts différents dans leur nature et leur comportement va induire des méthodes variées de calcul selon que l'on prendra en compte telle ou telle catégorie.  Ces méthodes sont complétées par des améliorations ponctuelles ou des techniques d'analyse destinées à la prise de décision dans un contexte spécifique.

3.1. Les méthodes de calculs de coûts

En reprenant le tableau 2.3-1, on peut agencer chaque type de coûts de manière différente. A partir de la matrice suivante, on débouche ainsi sur deux ensembles de méthodes fondées sur des calculs de coûts partiels ou de coûts complets :

CHARGES	DIRECTES	INDIRECTES
VARIABLES	1	2
FIXES	3	4

Tableau 3.1‑1 : éléments de typologie des méthodes de calcul des coûts

3.1.1.  Les calculs de coûts partiels

Une première partition consiste à conserver uniquement les charges variables comprises dans les cases 1 et 2 et à laisser par ailleurs l'ensemble des coûts fixes (cases 3 et 4). Cette opération débouche sur une première méthode, appelée méthode des coûts variables, connue également sous le vocable anglo-saxon de « direct costing »[1]. La méthode est surtout intéressante dans une optique prévisionnelle, car elle permet de calculer un seuil de rentabilité, c'est-à-dire un seuil de chiffre d'affaires ou de quantités vendues qui permet à l'entreprise de couvrir ses charges fixes et donc, de commencer à réaliser du bénéfice.

Une deuxième partition consiste à considérer les charges variables (1 + 2) augmentées des charges fixes directes (3). Ce calcul correspond à la méthode des coûts spécifiques, appelée également « direct costing évolué ». Cette méthode prolonge la précédente et son principal intérêt est de mieux appréhender la contribution d'un produit à l'absorption des charges fixes indirectes. En d'autres termes, une fois ce coût calculé, si la « marge sur coûts spécifiques », c'est-à-dire la différence entre le prix de vente du produit, les charges variables et les charges qui lui sont imputables en propre est encore positive, alors cela signifie que son exploitation permet d'absorber une partie des frais de structure. Il s'agit par conséquent, d'un outil précieux pour apprécier la rentabilité des produits et leur abandon éventuel.

Une troisième partition consiste à retenir uniquement les charges directes variables et fixes (1+ 3) laquelle permet de calculer une « marge sur coûts directs » qui peut être utilisée par exemple, pour estimer la marge dégagée par un établissement ou un magasin. Imaginons, une petite société qui distribue différents produits informatiques dans différentes villes sur la Côte d'Azur. La marge sur coûts directs, c'est-à-dire, la différence entre le chiffre d'affaires et l'ensemble des coûts directement supportés par un magasin permet de savoir si ce dernier est rentable et contribue à absorber les charges communes à la gestion de l'ensemble des magasins.

3.1.2.  Les méthodes de calcul en coûts complets

Elles correspondent à la prise en compte de tous les coûts, afin de calculer un coût de revient « complet » du produit. Elles permettent ainsi, de calculer une marge bénéficiaire par produit. On peut distinguer deux techniques de calcul : la comptabilité par « centre d'analyse » et la comptabilité « par activité ».

À côté de ces méthodes, d'autres techniques de calculs de coûts sont envisageables, sans que l'on puisse parler de « méthode ». Ces modes de calculs constituent, soit un prolongement des précédentes, soit plus généralement des techniques d'aide à la décision.

3.2. Améliorations et techniques ponctuelles d'aide à la prise de décision

3.2.1.  Les coûts standards et coûts préétablis

Ce sont des coûts souvent calculés à partir de coûts complets et qui ont vocation à établir des prévisions et des devis. Ils débouchent sur des calculs d'écarts, dont l'interprétation constitue un outil important du contrôle.

3.2.2.  L'imputation rationnelle des charges fixes

Il s'agit également d'un prolongement de la méthode des coûts complets. La technique présente l'avantage de moduler le calcul du coût complet des produits pour tenir compte de la variabilité des charges fixes unitaires.

3.2.3.  Le coût marginal

Le coût marginal correspond au coût d'une unité, d'un lot ou d'une supplémentaire fabriquée. Sa connaissance est essentielle en tant qu'outil d'aide à la décision. Il revêt une grande importance en raison de son rôle pivot au sein de la micro-économie.